DataScience Training
Keywords
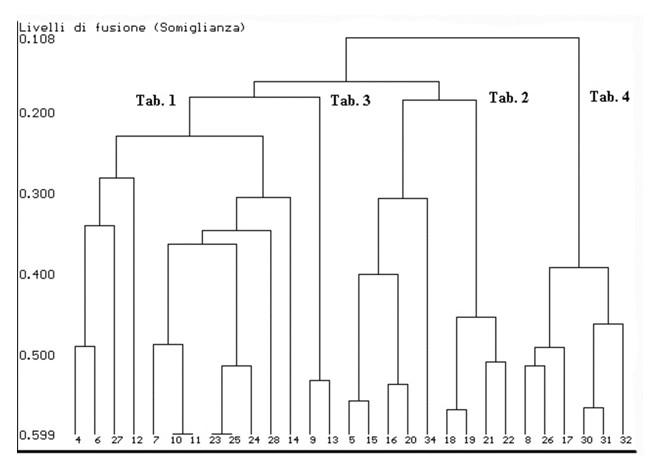
Statistical units, cluster, intra-cluster, inter-cluster, dissimilarity index, merge distance, dendogram.
Objectives/goals:The aim of this module is to introduce and explain the technique of Cluster Analysis.
At the end of this module you will be able to:
- Know the logic of Cluster Analysis
- Know the requirements
Conduct a Cluster Analysis
In this training module you will be presented the multidimensional analysis technique called Cluster Analysis, also called automatic group analysis.
Cluster analyses are used to group statistical units that have characteristics in common and assign them to categories not defined a priori. The groups that are formed must be as homogeneous as possible inside (intra-cluster) and heterogeneous outside (inter-cluster).
The application of this type of analysis is manifold: computer science, medicine, biology, marketing.
The last part of the module will be dedicated to the application of cluster analysis with the R software.
Related training material
 Play Audio
Play Audio