DataScience Training



Cluster-Analyse
Feedback form    |           |   Download:    |   


Clusteranalyse

Einleitung

Clusteranalyse Click to read  

Die Clusteranalyse ist eine multivariate Analysetechnik, die in vielen Bereichen eingesetzt werden kann: von der Informatik über die Medizin und die Biologie bis hin zur Archäologie und zum Marketing. Sie wird immer dann eingesetzt, wenn es darum geht, eine große Menge an Informationen in unterscheidbare Gruppen zu klassifizieren.
Goal Click to read  

Die Clusteranalyse wird verwendet, um statistische Einheiten (Datensätze) zu gruppieren, die gemeinsame Merkmale aufweisen. Diese gruppierten Einheiten werden dann Kategorien zugeordnet, welche nicht a priori definiert wurden.
Die gebildeten Gruppen (Cluster) müssen intra-cluster* möglichst homogen (oder ähnlich) und inter-cluster** möglichst heterogen (oder unähnlich) sein.

*innerhalb des Clusters
**außerhalb des Clusters bzw. zwischen zwei Cluster
 
Arten von Variablen Click to read  

In der Clusteranalyse verwenden wir sowohl:

- quantitative Variablen (numerisch) 

- qualitative Variablen (stellen Modalitäten dar wie z. B. Geschlecht, Bildungsstand, Familienstand usw.)
Clusteranalyse

Dissimilaritätsmatrix (oder Distanzmatrix) Click to read  

Die Distanzmatrix D ist nützlich, um zu wissen, wie viele statistische Einheiten sich voneinander unterscheiden, sie ist entscheidend für die Wahl der zu berücksichtigenden Variablen. 
Die Distanzmatrix mit den Dimensionen n x n ist eine symmetrische Matrix, die auf der größeren Diagonale alle 0 hat, weil der Abstand zwischen einem Punkt und sich selbst gleich Null ist. 
Vor der Erstellung der Distanzmatrix muss die Ausgangsmatrix standardisiert werden, damit jede Variable das gleiche Gewicht wie die anderen hat.
Um die Distanzmatrix D zu erhalten, muss man die Abstände zwischen den Punkten berechnen.
Je nach Art der quantitativen oder qualitativen Variablen, mit denen wir arbeiten, können diese Abstände auf unterschiedliche Weise berechnet werden.
 

Quantitative Variablen:

-  Euklidischer Abstand (empfindlich gegenüber Ausreißern)
- Manhattan-Distanz (sehr robust)
                                                                                                                                                                                  
                                                                                                                                                  

Qualitative Variablen:

Hier werden die Häufigkeiten berücksichtigt, dann die Ähnlichkeitsmatrix erstellt und schließlich werden die Übereinstimmungen und Unterschiede zwischen den Optionen berechnet.

Es gibt zwei Arten von Ähnlichkeitsindizes:

- M-Koeffizient (Simple Matching), für symmetrische binäre Variablen und
- Jaccard, für asymmetrische binäre Variablen.
 

 

 

 
Erstellen von Clustern Click to read  

Dank der Verknüpfungsregel können wir die Art der Verknüpfung (Linkage) wählen, die wir zur Bildung von Clustern verwenden werden:

- Single-Linkage
- Complete-Linkage
- Average-Linkage

Single-Linkage: 

Die Gruppen werden nach dem geringsten Abstand zwischen den Beobachtungen zusammengestellt. 
Diese Verbindung begünstigt die Homogenität der Elemente jeder Gruppe zum Nachteil der Differenzierung. 

 

Complete-Linkage:  
Die Gruppen werden nach dem kleinsten maximalen Abstand zwischen den Punkten zusammengestellt, d. h. es werden zunächst die größten Abstände zwischen den Gruppen berechnet und dann diejenigen ausgewählt, die den geringsten Abstand aufweisen. 
Diese Art der Verknüpfung hebt eher die Unterschiede zwischen den Gruppen als die interne Homogenität hervor.

Average-Linkage:  
Die Gruppen werden nach dem minimalen durchschnittlichen Abstand zusammengestellt, d. h. wir berechnen zunächst den durchschnittlichen Abstand zwischen allen
Beobachtungen und nehmen dann den minimalen Abstand zwischen ihnen. 
Diese Art der Verknüpfung ist weniger anfällig für Extremwerte und daher robuster.

 
Fusionsabstand und Dendogramm Click to read  

Nach der Auswahl der für unsere Analyse am besten geeigneten Verknüpfung und der Erstellung von Gruppen erstellen wir die grafische Darstellung: das Dendogramm.
Es stellt den Aggregationsgrad der Cluster nach ansteigenden Ordinaten dar. Die Punkte befinden sich auf der x-Achse und die Abstände auf der y-Achse.
  
 
Der Abstand zwischen den Clustern nimmt tendenziell zu, und aus diesem Grund wählen wir eine Stoppregel, die es uns erlaubt, die Anzahl der gewünschten Gruppen zu wählen. 
Dazu verwenden wir die Baumfälltechnik:
- Wir identifizieren die längsten Äste;
- Durch das Kriterium der Parsimonie (in der Regel liegen 4-5 homogene Cluster innerhalb und heterogene Cluster außerhalb);
- Mit einem Scree-Plot (wenn der Graph abflacht, oder wenn beim Übergang von g zu g+1 Gruppen ein starker Anstieg zu verzeichnen ist);
- Dabei ist auf Ausreißer zu achten (Cluster, die aus einem einzigen Punkt bestehen). 
 
 

 
Fallstudie zu R

Erstellen der Distanzmatrix Click to read  

Nachdem wir den Datensatz in R importiert haben, beginnen wir mit der Analyse der Cluster:

 
Choosing the Type of Link Click to read  

 

Mit Simple-Linkage erzielen wir folgendes Ergebnis:

 

 

Das gleiche Verfahren wird für Complete-Linkage und Average-Linkage durchgeführt.
Dann vergleichen wir die Ergebnisse und wählen die geeignetste Methode für die Analyse.

Im Vergleich der drei Ergebnisse ist Complete-Linkage am besten geeignet, da sie die Cluster besser unterteilt und eine zu große interne Homogenität auf Kosten der externen Heterogenität vermeidet. Sie verhindert auch die Bildung von Ausreißern, d. h. von Clustern, die aus einem einzigen Punkt bestehen.

 

 

 
Zusammenfassung

Zusammenfassung Click to read  


Keywords

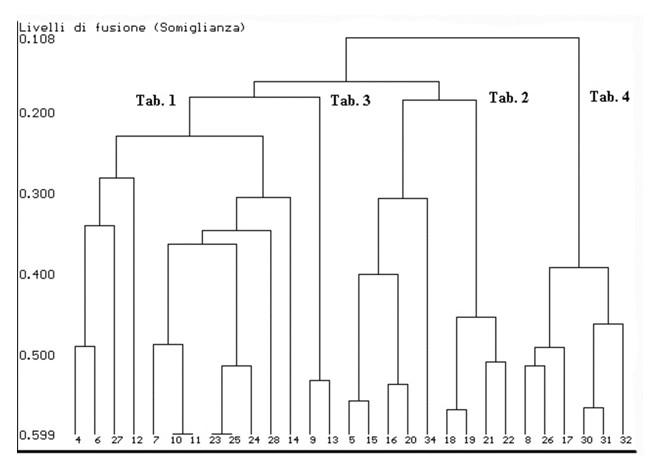
Statistische Einheiten, Cluster, Intra-Cluster, Inter-Cluster, Dissimilaritätsindex, Merge-Distanz, Dendogramm.

Objectives/goals:

Ziel dieses Moduls ist es, die Technik der Clusteranalyse einzuführen und zu erklären.

Am Ende dieses Moduls werden Sie in der Lage sein:

-    Die Logik der Clusteranalyse zu verstehen

-    Die Anforderungen zu kennen

-    Eine Clusteranalyse durchzuführen


 Description:

In diesem Modul lernen wir die mehrdimensionale Analysetechnik der Clusteranalyse kennen, die auch automatische Gruppenanalyse genannt wird.

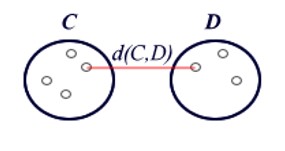
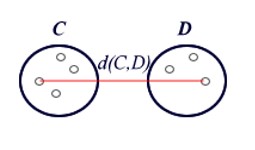
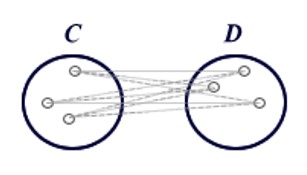
Clusteranalysen dienen dazu, statistische Einheiten, die gemeinsame Merkmale aufweisen, zu gruppieren und sie nicht a priori definierten Kategorien zuzuordnen. Die gebildeten Gruppen müssen innerhalb (Intra-Cluster) möglichst homogen und außerhalb (Inter-Cluster) heterogen sein.

Die Anwendungsmöglichkeiten dieser Art von Analyse sind vielfältig: Clusteranalysen werden z.B. in der Informatik, Medizin, Biologie, oder im Marketing genutzt.

Im letzten Teil des Moduls lernen wir, wie wir die Software R für Clusteranalysen einsetzen können.


Related training material

Partner

Università del Salento
Demostene Centro Studi
IHF
IWS
Universidad de Oviedo
ASE
WAI