|
Análisis de componentes principales (APC)
Introducción
Introducción Click to read 
El análisis de componentes principales (APC) es una técnica de análisis estadístico multivariante para la reducción de la dimensionalidad en la práctica se usa cuando dentro de un conjunto de datos hay muchas variables y están correlacionadas, con el fin de reducir su número, perdiendo la cantidad de información más pequeña posible.
APC tiene precisamente el objetivo de maximizar varianza , calculando el peso a atribuir a cada a partir de variable para poder concentrarlas en una o más variables nuevas ( llamadas principal componentes ) que será una combinación lineal de las iniciales variables.
Requisitos del análisis de componentes principales
Requisitos del análisis de componentes principales Click to read 
Análisis de variables
|
Para entender si tiene sentido realizar el análisis de componentes principales, es importante analizar las variables a utilizar para claras algunas de sus características. En concreto, las variables deben cumplir los siguientes requisitos:
|
 |
- Las variables deben ser cuantitativas
|
Un APC es válido solo cuando las variables son numéricas. En caso de diferente unidades de medida, debemos estandarizar las variables antes. Sin embargo, en algunos casos se emplea también para variables de "escala de Likert " y para variables " binarias". A pesar de que numéricamente los resultados son muy similares, en estos casos sería preferible utilizar métodos alternativos.
|
 |
- Debe haber una correlación lineal entre las variables
Lo primero que hay que hacer para aplicar un APC es calcular la matriz de varianzas / covarianzas (o matriz de correlación de Pearson). El APC, de hecho, es una técnica que se puede utilizar cuando los supuestos de la correlación lineal de Pearson se cumplen. Los coeficientes de correlación de Pearson informan sobre la dirección y la intensidad de la relación lineal entre fenómenos: cuanto más cercano sea el coeficiente a cero, más débil es la relación y cuanto más cerca llega a -1 o +1, más fuerte es la relación. En APC, valores aceptables para estos indicadores son R>0.3 o R<-0.3. Si una variable tenía correlación coeficientes muy cerca de 0 con todas los demás variables, entonces esa variable no debería estar incluida en el AP, pues su fusión con otras resultará en una pérdida muy alta de información y esto es algo eso es generalmente a evitar.
- Falta de valores atípicos
|
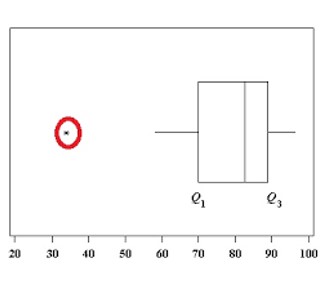
Como con todo lo basado en el análisis de varianza análisis, los valores atípicos individuales pueden afectar los resultados si son muy grandes y si el tamaño de la muestra es pequeño.
Con este fin, es útil crear diagramas de caja o diagramas de dispersión, a partir de los cuales es posible deducir relaciones lineales entre pares de variables.
|
 |
Tamaño de muestra bastante grande
|
Aunque no hay un valor límite claro, generalmente es recomendable tener al menos 5-10 obseervaciones para cada variable que se desea incluir en el APC. Por ejemplo, si se quiere tratar de resumir 10 variables con nuevos componentes, sería recomendable tener una muestra de al menos menos 150 observaciones.
|
 |
Cómo realizar APC
Cómo realizar APC Click to read 
- Adecuación de la muestra
Después de verificar los requisitos del conjunto de datos, y verificarse que las variables tienen las características correctas para poder realizar el análisis de componentes principales, aquí están los diferentes pasos para realizarlo:
Comprobar la adecuación de la muestra:
- La prueba de Kaiser-Meyer- Olkin, (KMO), que establece si las variables considerados son realmente consistentes para el uso de un análisis de componentes principales. Este índice puede tomar valores entre 0 y 1 y, para que un análisis de componentes principales tenga sentido , debe tener un valor en el menos mayor que 0.5.
Este índice se puede calcular como un tod para todas las variables incluido en el APC.
- Prueba de esfericidad de Bartlett: es un test que tiene como hipótesis nula que la matriz de correlación coincide con la matriz identidad. Si es así, no tendría sentido realizar un APC puesto que las variables no están relacionadas entre sí. Como en todos los tests, el valor en el que detenerse para decidir si se rechaza la hipótesis nula o no es el p-valor . En este caso, para que el modelo sea considerado válido , un valor de p más bajo de 0,05 debe ser alcanzado. En este caso, la hipótesis nula puede ser rechazada a un nivel de significación del 5%.
Extracción de los principales componentes Click to read 
La parte crucial de APC es establecer el número de factores que mejor puede representar el conjunto de variables. Para entender mejor este concepto, imagina un conjunto de datos como una ciudad desconocida, y cada componente principal es una calle en esta ciudad. Si queremos conocer esta ciudad, ¿cuántas calles hemos de visitar? Probablemente comenzaríamos desde la calle central (el primer componente principal ) y luego exploraríamos otras calles.
¿Pero cuántas para decir que se conoce bien una ciudad? La cantidad de calles a visitar varía según el tamaño de la ciudad y cómo de similares o diferentes son entre sí. Del mismo modo , el número de componentes a extraer depende de cuántas variables tenemos y cómo de similares son entre ellas. De hecho, cuanto más correlacionadas estén, menor es el número de componentes necesarios para obtener un buen conocimiento de las variables iniciales. Por el contrario, cuanto menos correlacionadas están, mayor es el número de componentes que se extraerán para tener información precisa sobre el conjunto de datos.
Los criterios utilizados para elegir el número de componentes son esencialmente dos: valores propios mayores que 1 y análisis paralelo:
- Valores propios mayores que 1
|
De acuerdo con esta regla, aquellos componentes a los que se les asigna un valor propio mayor que 1 se eligen.
El valor propio es un número que muestra que parte de la varianza es explicada por el componente: ya que inicialmente la varianza explicada por cada variable es igual a 1, no tiene sentido elegir un componente (que es una combinación de variables ) con varianza menos que 1.
Un valor propio alto corresponde a una mayor varianza y un software como R genera una tabla con los valores propios ordenados de forma decreciente. Por lo tanto, el primero estará siempre asociado con el factor más importante.
|
 |
- Proporción de varianza explicada
Siguiendo esto criterio, los componentes a extraer deben al menos el 70% de la variabilidad de partida. Además , cada uno de los componentes a extraer debería producir un significativo aumento en el total varianza (por ejemplo , al menos un 5% o un 10% más de la variabilidad explicada anteriormente).
- Scree Plot
|
Este método se basa en un gráfico en el que los valores propios se muestran en el eje vertical y todos lo posible componentes a extraer en el eje horizontal (que por lo tanto será igual al número de variables ). Al unir los puntos se obtiene una línea que en algunas partes tienen forma cóncava y en otros convexa.
|
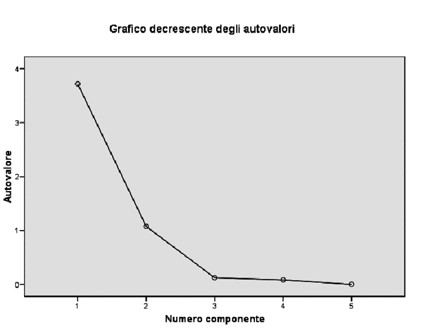 |
Como puede verse en el gráfico , los componentes se enumeran en el eje x , mientras que los valores propios están en el eje y . Cuando la curva en este gráfico hace un "codo" se traza una línea, y se toman en consideración solo los factores que están por arriba.
En el gráfico anterior, por ejemplo, puede verse que el número de puntos por encima del codo es 2.
La parte final de APC consiste en dar un nombre (interpretación) a los componentes encontrados.
ACP con R
ACP con R Click to read 
Con un software estadístico (como SPSS, Jamovi y R), realizar un APC es una operación muy simple. Unos pocos clics son suficientes para poder obtener una salida a interpretar. No existe, por tanto, ningún software preferible a los demás ya que es una técnica muy utilizada y todos los programas estadísticos permiten realizarla fácilmente y sin tener que realizar ningún cálculo manual. Sin embargo, en este módulo mostraremos cómo realizar APC con el software R.
El proceso para implementar APC en R se representará en el power point adjunto a este módulo , a saber :
- Realización de todos los pasos que se basen en pruebas matriciales, geométricas y estadísticas;
- A través del comando directo ACP del paquete FactoMineR.
En este módulo solo se presentará el paquete FactoMineR.
FactoMineR es capaz de llevar a cabo el procedimiento ACP mediante la reducción de la dimensionalidad de los datos a dos o tres dimensiones, que por tanto se pueden mostrar gráficamente con una mínima pérdida de información. Esto se puede hacer usando un simplemente el comando PCA, insertando la matriz de datos objeto de análisis entre paréntesis
X <- as.matrix(DATASET)
library(FactoMineR)
res.pca = PCA(DATASET)
con el comando summary podemos ver la importancia de los componentes en términos de desviación estándar, proporción de explicada varianza y la varianza acumulada explicada, tanto para individuos como para variables.
summary(res.pca)
Con el comando head:
head(ris.pca$eig)
se puede calcular la importancia de los valores propios. El comando, de hecho, nos proporcionará los valores de los autovalores, el porcentaje de la varianza explicada y la varianza explicada acumulada para cada componente.
Ejemplo en R:
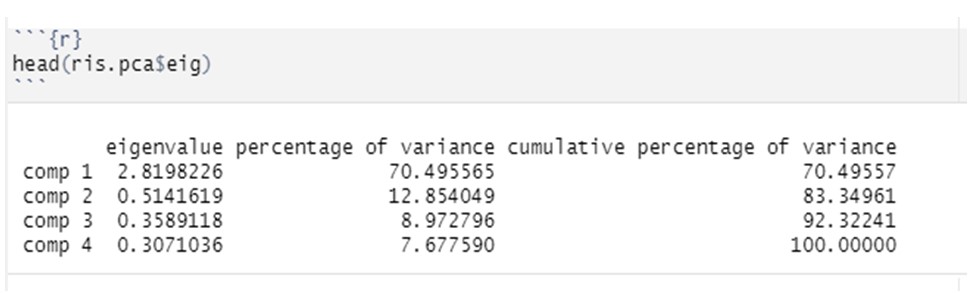
Finalmente, para poder dibujar el gráfico de los valores propios, debemos insertar el objeto de análisis entre paréntesis
barplot(res.pca$eig[,1], main="Eigenvalues’ scree-plot")
con el comando principal indicaremos el título del gráfico.
Ejemplo en R:
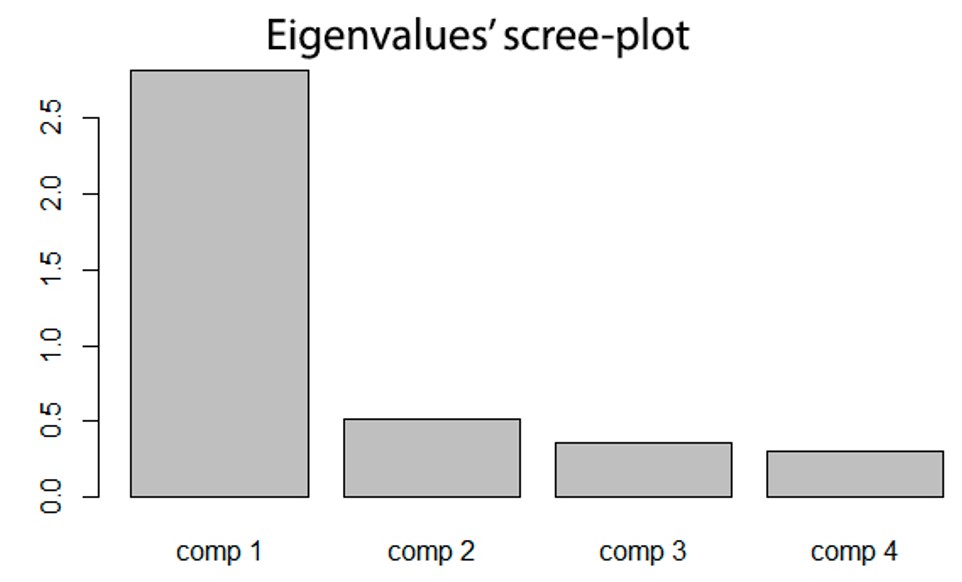
Otro paquete útil para APC (no estudiado en este módulo) es factoextra, que proporciona algunas funciones fáciles de usar para extraer y visualizar los resultados obtenidos de análisis multivariantes, incluyendo APC (análisis de componentes principales), CA (análisis de correspondencias simple), MCA (análisis de correspondencias múltiple), MFA (análisis factorial múltiple), HMFA (análisis factorial múltiple jerárquico).
|
 Reproducir el audio
Reproducir el audio 



















