|
Analisi in componenti principali (ACP)
Introduzione
Introduzione Click to read 
Obiettivo
l'obiettivo di questo modulo è introdurre e spiegare la tecnica dell'Analisi delle Componenti Principali.
Alla fine di questo modulo sarai in grado di:
 Conoscere la logica dell’ACP; Conoscere la logica dell’ACP; Conoscere i requisiti; Conoscere i requisiti; Condurre un ACP. Condurre un ACP.Definizione
► L’analisi delle componenti principali (ACP) è una tecnica statistica di analisi multivariata per la riduzione delle dimensioni. In pratica, si utilizza quando all’interno di un dataset ci sono molte variabili correlate tra di loro e si vorrebbe ridurne il numero perdendo la minore quantità di informazione possibile.
► L’ACP ha proprio l’obiettivo di massimizzare la varianza, calcolando il peso da attribuire ad ogni variabile di partenza per poterle concentrare in una o più nuove variabili (dette componenti principali) che saranno combinazione lineare delle variabili di partenza
L’ACP nella vita reale
► Nelle scienze sociali ci si trova molto spesso di fronte a ricerche in cui vi è una sovrabbondanza di misurazioni (Indicatori) nel tentativo di comprendere meglio il fenomeno che si sta studiando.
► Un esempio vicino al mondo universitario potrebbe essere le valutazioni espresse da studenti con riferimento ad un certo corso e che prevede diversi variabili. Spesso per misurare il gradimento di un corso si utilizzano un alto numero di variabili che va dalla valutazione delle dispense, del materiale utilizzato, dal grado di confort delle aule, gli orari, il numero di ore dedicate a ricevimento o tutoraggio e cosi via. L’ACP permetterà di ridurre le Dimensioni e rendere l’analisi più semplificata.
I requisiti dell’ACP
I requisiti dell’ACP Click to read 
Analisi delle Variabili
|
Affinché sia sensato condurre l’analisi delle componenti principali, è importante analizzare le variabili da utilizzare per avere chiare alcune loro caratteristiche. Nello specifico le variabili devono avere i seguenti requisiti
|
 |
Le variabili devono essere di tipo Quantitativo
- Deve esserci una Correlazione lineare tra le variabili
 La prima operazione da fare quando si effettua un’ACP è calcolare la matrice di varianza/covarianza o la matrice di correlazione di Pearson La prima operazione da fare quando si effettua un’ACP è calcolare la matrice di varianza/covarianza o la matrice di correlazione di Pearson l’ACP, infatti, è una tecnica utilizzabile quando sono rispettate le ipotesi dell’indice di correlazione lineare di Pearson l’ACP, infatti, è una tecnica utilizzabile quando sono rispettate le ipotesi dell’indice di correlazione lineare di Pearson
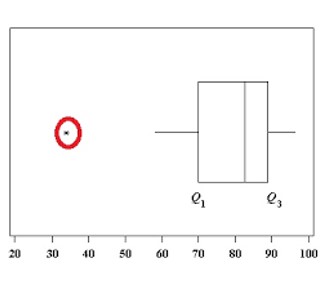
- Assenza di outliers
 Come per tutte le analisi basate sulla varianza, singoli valori anomali possono influenzare i risultati soprattutto se molto estremi e se la numerosità campionaria è bassa. Come per tutte le analisi basate sulla varianza, singoli valori anomali possono influenzare i risultati soprattutto se molto estremi e se la numerosità campionaria è bassa.
 A tal fine è utile realizzare dei boxplot oppure grafici a dispersione, detti scatterplot, dai quali è possibile dedurre relazioni lineari tra coppie di variabili. A tal fine è utile realizzare dei boxplot oppure grafici a dispersione, detti scatterplot, dai quali è possibile dedurre relazioni lineari tra coppie di variabili. |
 |
Numerosità del campione abbastanza elevata
Come condurre l’ACP
Come condurre l’ACP Click to read 
- Adeguatezza del campione
Per verificare l’adeguatezza del campione si possono svolgere alcuni test come:
 Il test Kaiser-Meyer-Olkin, (KMO), che stabilisce se effettivamente le variabili considerate sono coerenti per l’utilizzo di un’analisi delle componenti principali. Questo indice può assumere valori compresi tra 0 e 1 e, affinché abbia senso effettuare un’analisi delle componenti principali, deve avere un valore almeno superiore a 0,5. Il test Kaiser-Meyer-Olkin, (KMO), che stabilisce se effettivamente le variabili considerate sono coerenti per l’utilizzo di un’analisi delle componenti principali. Questo indice può assumere valori compresi tra 0 e 1 e, affinché abbia senso effettuare un’analisi delle componenti principali, deve avere un valore almeno superiore a 0,5.
 Test di sfericità di Bartlett: è un test d’ipotesi che ha come ipotesi nulla quella che la matrice di correlazione coincida con la matrice identità. Se così fosse, non avrebbe senso performare una ACP in quanto significherebbe che le variabili non sono per nulla correlate linearmente tra di loro. Test di sfericità di Bartlett: è un test d’ipotesi che ha come ipotesi nulla quella che la matrice di correlazione coincida con la matrice identità. Se così fosse, non avrebbe senso performare una ACP in quanto significherebbe che le variabili non sono per nulla correlate linearmente tra di loro.
- Estrazione delle componenti principali
|
Per comprendere meglio questo concetto, immagina che il tuo dataset sia una città a te sconosciuta!
Ogni componente principale è una strada di questa città. Se tu volessi conoscere questa città, quante strade visiteresti? Probabilmente partiresti dalla via centrale (la prima componente principale) e poi ti addentreresti in altre vie.
Ma in quante?
|
 |
Per poter dire di conoscere a sufficienza una città, ovviamente il numero di vie da visitare cambia a seconda delle dimensioni della città e di quante le vie sono simili o diverse tra loro.
Allo stesso modo, il numero di componenti da estrarre dipende da quante variabili hai scelto di includere all’interno dell’analisi delle componenti principali e da quanto queste sono simili tra loro.
Più sono correlate infatti, minore sarà il numero di componenti principali necessario per ottenere una buona conoscenza delle variabili di partenza. Al contrario, meno sono correlate, maggiore sarà il numero di componenti principali da estrarre per poter avere un’informazione accurata del dataset.
Come condurre l’ACP: I Criteri Click to read 
- Autovalori Maggiori di 1
|
Secondo questa regola, si scelgono quelle componenti a cui è associato un autovalore superiore a 1.
L’autovalore è un numero che fornisce la varianza spiegata dalla componente: siccome inizialmente la varianza spiegata da ogni singola variabile è pari a 1, non avrebbe senso prendere una componente (che è una combinazione di variabili) con varianza inferiore a 1.
|
 |
- Proporzione di Varianza Spiegata complessiva
Seguendo questo criterio, le componenti da estrarre devono garantire che almeno il 70% della variabilità complessiva delle variabili di partenza non venga persa.
Inoltre, ogni singola componente da estrarre dovrebbe apportare un incremento di rilievo alla varianza complessiva (ad esempio, almeno un 5% o un 10% in più di variabilità spiegata).
- Scree Plot
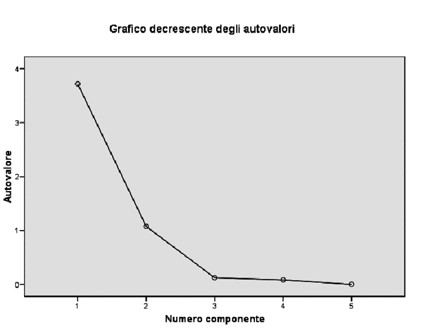
Questo metodo, si basa su un grafico in cui sull’asse verticale sono riportati i valori degli autovalori e sull’asse orizzontale tutte le possibili componenti da estrarre (che saranno quindi in numero pari alle variabili di partenza). Unendo i punti si otterrà una linea spezzata che in alcune parti avrà una forma concava ed in altri convessa.
|
 Come è possibile vedere dal grafico sull’asse x sono elencate le componenti, mentre sull’asse y ci sono gli autovalori. Come è possibile vedere dal grafico sull’asse x sono elencate le componenti, mentre sull’asse y ci sono gli autovalori.
 Quando la curva di questo grafico fa un “gomito” è il momento per tracciare una linea, e prendere in considerazione solo i fattori che stanno sopra. Quando la curva di questo grafico fa un “gomito” è il momento per tracciare una linea, e prendere in considerazione solo i fattori che stanno sopra.
 Dal grafico che puoi vedere qui, ad esempio, si vede che il numero di punti che si trovano sopra al gomito è 2. Dal grafico che puoi vedere qui, ad esempio, si vede che il numero di punti che si trovano sopra al gomito è 2.
|
 |
- Nominarle
|
La parte conclusiva dell’ACP consiste nel dare un nome alle singole componenti principali trovate.
|
 |
Come condurre l’ACP: Un Caso Studio Click to read 
Consideriamo un caso di studio. Supponiamo di avere la seguente rilevazione di performance aziendale su 10 famose aziende.
|
•ECON.PRO -> economic profit, differenziale tra rendimento del capitale investito ed il suo costo
•CASH -> cash flow sul fatturato in %
•LAVOR.VA -> costo del lavoro
sul valore aggiunto, in%
•ROE -> return on equity, utile
•netto sul patrimonio, in%
•INDE.CAP -> indebitamento
sul capitale proprio
•FATTURATO
|
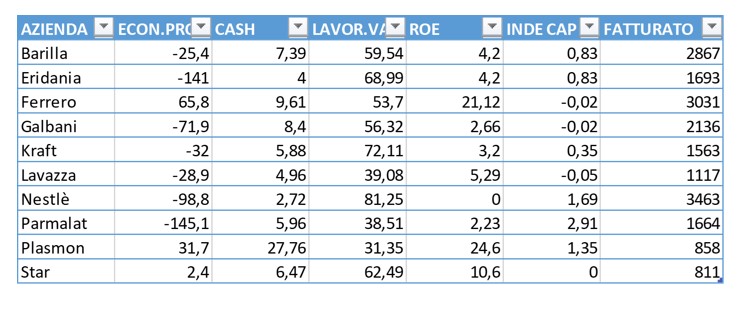 |
Dal momento che i dati sono espressi in unità di misura molto diverse, passiamo alla matrice dei dati standardizzata
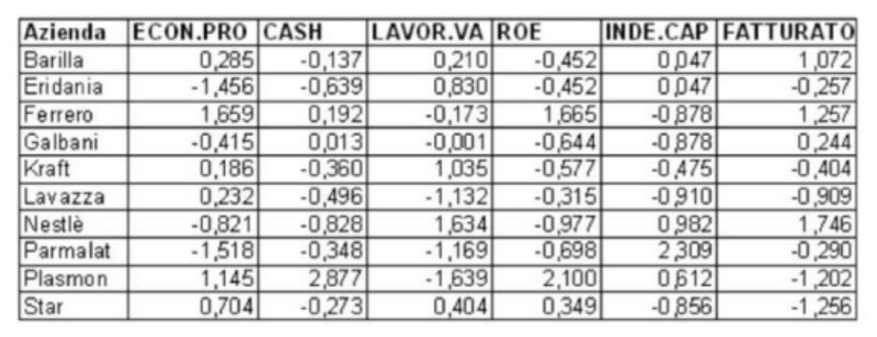
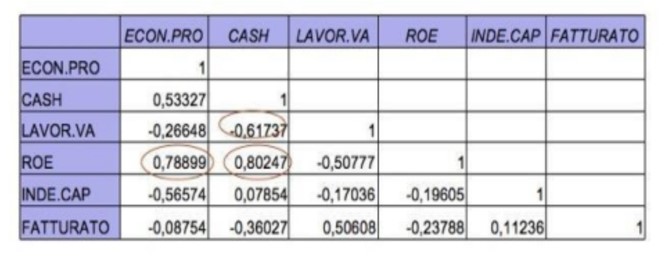
Come già detto l'osservazione della matrice di correlazione è una fase importante: se tutte le variabili fossero non correlate tra di loro non avrebbe senso procedere con l’ACP, infatti si avrebbero tante componenti quante variabili osservate. Se invece alcune sono molto correlate se ne deve prendere una sola.
Dalla tabella si evince come il ROE sia correlato positivamente col Cash Flow e la variabile economic profit, tuttavia le consideriamo nell’analisi.
|
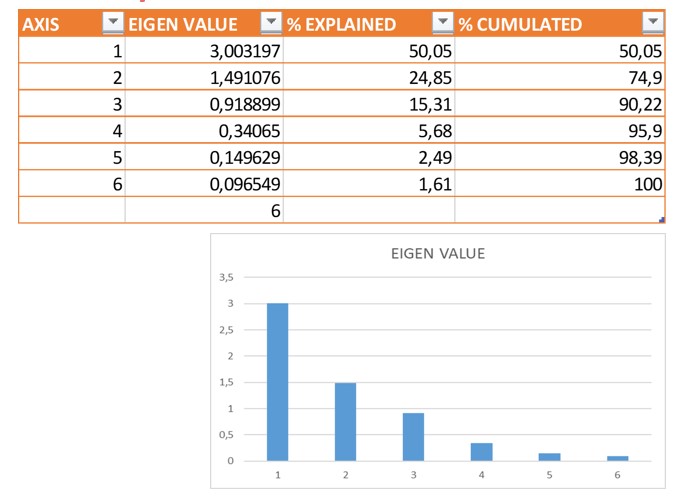
•Si calcolano autovalori, autovettori e si analizza la percentuale di varianza spiegata dagli autovalori attraverso lo screeplot.
•Gli autovalori maggiori di 1 in questo caso spiegano il 74,9% della varianza originaria
•E’ Possibile estrarre 2 Componenti in quanto le prime 2 dimensioni raggiungono Il 75% di varianza cumulata
|
|
|
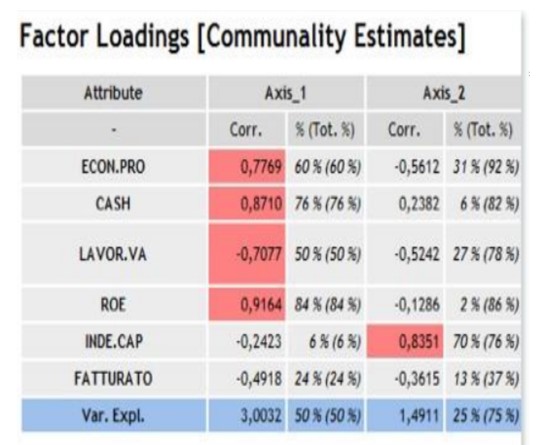
Per comprendere il ruolo giocato da ogni variabile nella costruzione dei fattori, e quindi per avere materiale su cui riflettere per comprendere il significato degli assi, si può analizzare la comunalità, che ci dice quanto ciascuna variabile è correlata con l’asse.
Si può notare che le variabili maggiormente correlate tra loro sono quelle che determinano il primo asse. Tale asse è il più importante perché è quello che riassume la massima variabilità. E la quantità di variabilità spiegata è influenzabile dalla correlazione tra le variabili originarie. Le variabili correlate con il primo asse suggeriscono di interpretare lo stesso come una sintesi di redditività (C1): a destra vi è una redditività alta, a sinistra una redditività bassa.
Il secondo asse discrimina sull’indebitamento (C2): in alto si posizioneranno le aziende ad alto tasso di indebitamento, in basso quelle che sono meno indebitate
|
 |
Come è possibile vedere dal Grafico nella slide successiva:
•Sul piano cartesiano le due componenti principali estratte rappresentano gli assi
•mentre gli Individui (in questo caso le aziende) sono proiettate sul piano.
•Esse si trovano più vicine ai fattori a seconda di quanto hanno contribuito a determinarli.
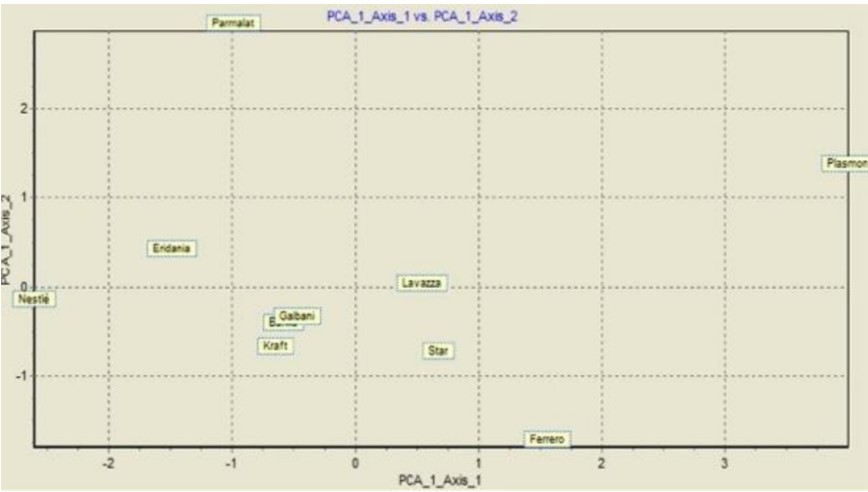
L’interpretazione: Alcune di esse si posizionano in zone diametralmente opposte:
● in basso a destra c’è la Ferrero che risulta essere l’azienda più sana, poiché ha un indebitamento negativo, quindi fa fronte agli impegni finanziari col capitale proprio, e una discreta redditività
● nel quadrante in alto a destra, si distingue la Plasmon che se pur fortemente indebitata ha un’altissima redditività.
● nel quadrante in basso a sinistra sono presenti quelle aziende che operano in mercati saturi in cui sono leader; inoltre, trovandosi vicino all’origine degli assi, mostrano di aver sotto controllo la situazione finanziaria, ed avendo un indebitamento negativo hanno a disposizione riserve di capitali pronte per essere utilizzate per far fronte alle esigenze del mercato o per intraprendere azioni di penetrazioni in business ad alta redditività
● Infine, in alto a sinistra, troviamo la Parmalat: questa mostra di avere la situazione peggiore. Ha un forte indebitamento e una redditività negativa, quindi, tale impresa deve necessariamente ripensare al suo sistema di business per evitare il rischio di insolvenza
Riassumendo
Riassumendo Click to read  |
 Riprodurre l’audio
Riprodurre l’audio