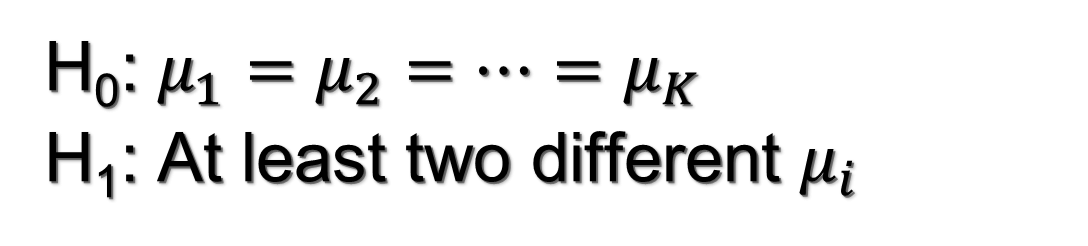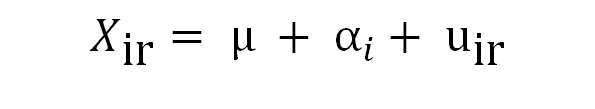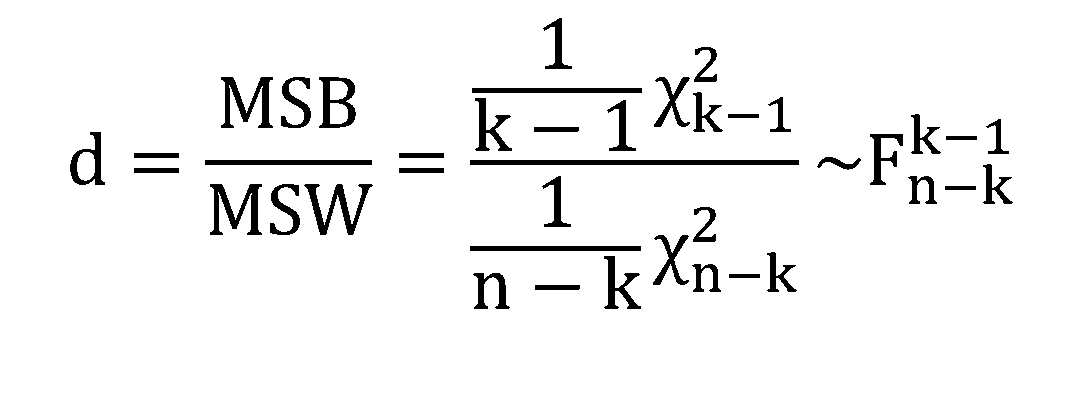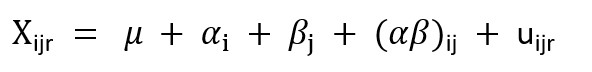DataScience Training
Keywords
Analisi multivariata, variabilità interna e tra gruppi, test di ipotesi, modelli lineari
Objectives/goals:Lo scopo di questo modulo è presentare i concetti di base dell'analisi della varianza a uno e due fattori (ANOVA), che può essere intesa come un modello lineare di base
Alla fine di questo modulo sarai capace di:
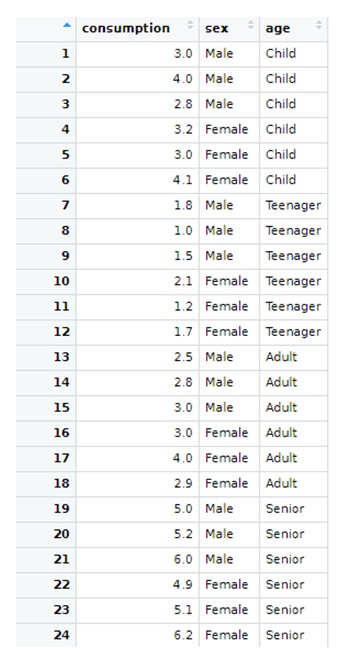
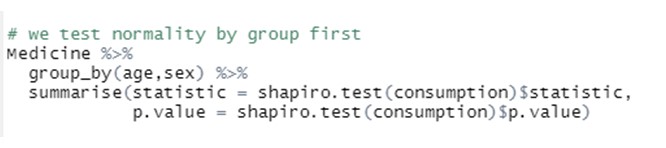
- Capire come ANOVA può essere utile per testare se ci sono differenze tra il valore medio di una variabile continua tra diversi livelli di una o più variabili categoriali.
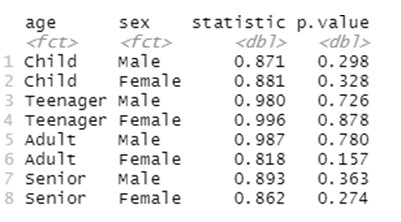
- Comprendere e identificare le condizioni necessarie per applicare queste tecniche.
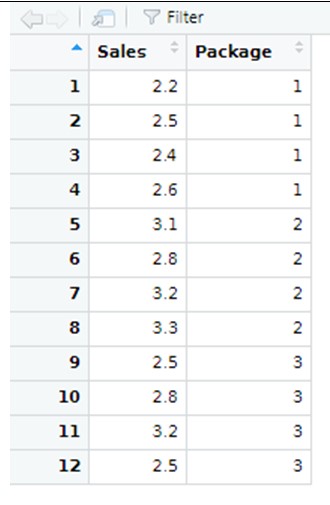
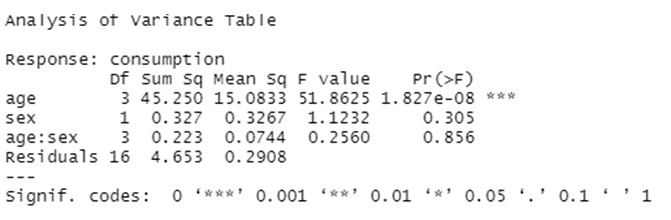
- Condurre analisi della varianza a una o più vie e interpretare i risultati ottenuti.
In questo modulo formativo verrai introdotto all'uso della modellazione lineare di base per capire come le differenze medie possono essere attribuite o meno all'effetto di variabili categoriali.
L'analisi qui presentata è alla base della regressione lineare, che considera anche l'effetto delle variabili continue. Le tecniche descritte in questo modulo formativo si limitano al caso di variabili categoriali (qualitative). A questo proposito, puoi affrontare i contenuti di questo modulo come un'introduzione al Modello lineare generalizzato (MLG) che utilizza solo fattori categoriali per spiegare la variabilità in una variabile (continua) di interesse.
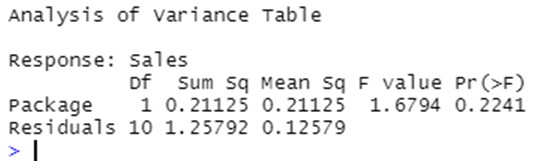
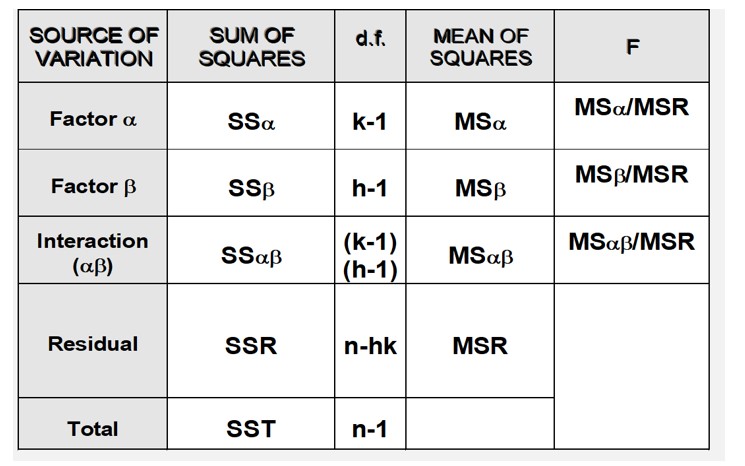
La procedura qui presentata si basa sulla scomposizione della variabilità totale misurata nel campione in diverse fonti: alcune sono residuali (o non spiegate dai fattori considerati) mentre altre provengono da una parte sistematica riconducibile alle diverse categorie dei fattori categoriali.
NEWBOLD, P. et al. (2008): Statistics for Management and Economics, (6th edition) Ed. Prentice Hall. Chapter 17, pp. 635-661
Related training material
 Riprodurre l’audio
Riprodurre l’audio