|
Hauptkomponentenanalyse (Principal Components Analysis, PCA)
Einleitung
Einleitung Click to read 
Ziele
Das Ziel dieses Moduls ist es, die Technik der Hauptkomponentenanalyse einzuführen und zu erklären.
Wir werden in diesem Modul lernen:
✔Die Logik der PCA zu verstehen;
✔Die erforderlichen Kriterien zu kennen;
✔Eine PCA durchzuführen.
Definitionen
⮚Die Hauptkomponentenanalyse (PCA) ist eine statistische Technik der multivariaten Analyse zur Größenreduktion. In der Praxis wird sie angewendet, wenn es in einem Datensatz viele miteinander zusammenhängende Variablen gibt und man die Anzahl reduzieren möchte, wobei so wenig wie möglich an Information verloren gehen soll.
⮚Die PCA hat das Ziel, die Varianz zu maximieren, indem sie das Gewicht berechnet, das jeder Ausgangsvariable zugeordnet werden soll, um sie in einer oder mehreren neuen Variablen (Hauptkomponenten genannt) zu konzentrieren, die eine lineare Kombination der Ausgangsvariablen sind
Anwendung der PCA im Alltag
❖In den Sozialwissenschaften sieht man häufig Forschungen, bei denen es eine Überfülle an Messungen (Indikatoren) gibt, um das untersuchte Phänomen besser zu verstehen.
❖Ein Beispiel, in dem PCA angewendet werden kann, sind die Bewertungen, die von Studierenden in Bezug auf einen bestimmten Kurs abgegeben werden, wobei mehrere Variablen verwendet werden. Oft werden viele Variablen verwendet, um die Zufriedenheit mit einem Kurs zu messen, wie z.B. die Bewertung der Lehrbücher, des verwendeten Materials, des Komforts der Klassenzimmer, der Stundenpläne, der Anzahl der Stunden, die der Betreuung oder Nachhilfe gewidmet sind, und so weiter. Die PCA wird die Dimensionen reduzieren und die Analyse vereinfachen
Vorraussetzungen für die PCA
Vorraussetzungen für die PCA Click to read 
Variablenanalyse
|
Um die Hauptkomponentenanalyse durchzuführen, ist es wichtig, die zu verwendenden Variablen zu analysieren, um einige ihrer Eigenschaften zu verstehen. Insbesondere müssen die Variablen die folgenden Anforderungen erfüllen:
|
 |
Variablen müssen quantitativ sein
|
✔Eine PCA ist nur dann möglich, wenn die Variablen numerisch sind.
✔Wenn die Merkmale unterschiedliche Maßeinheiten haben, müssen wir die Variablen standardisieren, bevor wir fortfahren.
In einigen Fällen wird PCA jedoch auch für Variablen auf einer "Likert-Skala" oder für "binäre Variablen" verwendet. Obwohl die Ergebnisse numerisch sehr ähnlich sind, ist es in diesen Fällen ratsam, alternative Methoden zu verwenden |
 |
Es muss eine lineare Korrelation zwischen den Variablen vorliegen.
✔Der erste Schritt bei der Durchführung einer PCA besteht darin, die Varianz-Kovarianz-Matrix oder die Pearson-Korrelationsmatrix zu berechnen
✔Die PCA ist eine Technik, die angewendet werden kann, wenn die Annahmen des linearen Korrelationsindexes nach Pearson erfüllt sind
Keine Ausreisser sind vorhanden
|
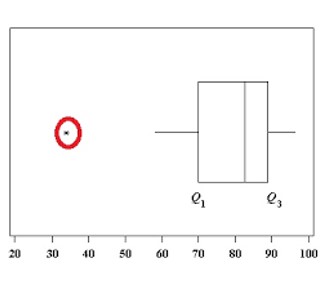
✔Wie bei allen Analysen, die auf der Varianz basieren, können einzelne Ausreißer die Ergebnisse beeinflussen, insbesondere wenn sie sehr extrem sind und die Stichprobengröße klein ist.
✔Zu diesem Zweck ist es nützlich, Boxplots oder Scatterplot-Diagramme zu erstellen, aus denen lineare Beziehungen zwischen Paaren von Variablen abgeleitet werden können.
|
 |
Ausreichend große Stichprobengröße
|
✔Es gibt keinen eindeutigen Schwellenwert, aber im Allgemeinen wird empfohlen, mindestens 5-10 statistische Einheiten für jede Variable zu haben, die in die PCA aufgenommen werden soll.
✔Wenn beispielsweise versucht wird, 10 Variablen mit neuen Komponenten zusammenzufassen, wäre es ratsam, eine Stichprobe von mindestens 150 Beobachtungen zu haben.
|
 |
Durchführung einer PCA
Durchführung einer PCA Click to read 
Angemessenheit der Stichprobe
Um die Angemessenheit der Stichprobe zu überprüfen, können verschiedene Tests durchgeführt werden, wie zum Beispiel:
✔Der Kaiser-Meyer-Olkin-Test (KMO), der feststellt, ob die betrachteten Variablen tatsächlich konsistent für die Verwendung einer Hauptkomponentenanalyse sind. Dieser Index kann Werte zwischen 0 und 1 annehmen. Damit eine Hauptkomponentenanalyse sinnvoll ist, sollte er mindestens den Wert 0,5 aufweisen.
✔Der Bartlett-Test auf Sphärizität ist ein Hypothesentest mit der Nullhypothese, dass die Korrelationsmatrix mit der Identitätsmatrix übereinstimmt. Wenn dies der Fall wäre, würde es keinen Sinn machen, eine PCA durchzuführen, da dies bedeutet, dass die Variablen überhaupt nicht linear miteinander korreliert sind.
Extraktion der Hauptkomponenten
|
Um dieses Konzept besser zu verstehen, stellen wir uns vor, unser Datensatz sei eine uns unbekannte Stadt und jede Hauptkomponente sei eine Straße in dieser Stadt.
Wenn wir diese Stadt kennenlernen möchten, wie viele Straßen würden wir besuchen?
Wir würden wahrscheinlich mit der zentralen Straße (der ersten Hauptkomponente) beginnen und dann andere Straßen erkunden.
Aber wie viele Straßen sollten es sein?
|
 |
Um eine Stadt gut genug zu kennen, hängt natürlich die Anzahl der Straßen, die man besuchen muss, von der Größe der Stadt und davon ab, wie ähnlich oder unterschiedlich die Straßen sind.
Ebenso hängt die Anzahl der zu extrahierenden Komponenten davon ab, wie viele Variablen wir in der Hauptkomponentenanalyse ausgewählt haben und wie ähnlich sich diese Variablen sind.
Tatsächlich benötigt man für gut korrelierte Variablen weniger Hauptkomponenten, um eine gute Kenntnis der Ausgangsvariablen zu erlangen. Im Gegensatz dazu benötigt man für weniger korrelierte Variablen eine größere Anzahl an Hauptkomponenten, um eine genaue Kenntnis des Datensatzes zu haben.
Durchführung einer PCA: Die Kriterien Click to read 
Eigenwerte größer als 1
|
Nach dieser Regel wählen wir die Komponenten aus, die einen Eigenwert größer als 1 haben.
Der Eigenwert ist eine Zahl, die die durch die Komponente erklärte Varianz wiedergibt: Da die anfängliche Varianz, die durch jede einzelne Variable erklärt wird, gleich 1 ist, wäre es nicht sinnvoll, eine Komponente (die eine Kombination von Variablen ist) mit einer Varianz von weniger als 1 zu wählen.
|
 |
Anteil der insgesamt erklärten Varianz
Nach diesem Kriterium behalten wir die Hauptkomponenten, die kumulativ mindestens 70% der Varianz erklären.
Darüber hinaus sollte jede einzelne extrahierte Komponente einen signifikanten Anstieg der Gesamtvarianz bieten (z. B. einen Anstieg um mindestens 5% oder 10% der erklärten Variabilität).
Scree Plot
|
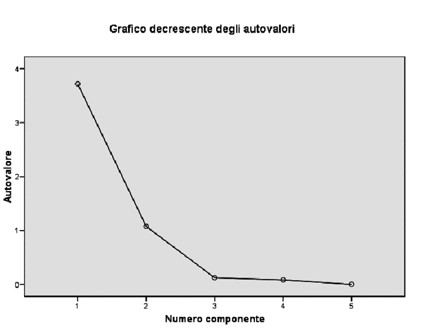
Diese Methode basiert auf einem Diagramm, bei dem die Werte der Eigenwerte auf der vertikalen Achse und alle möglichen zu extrahierenden Komponenten auf der horizontalen Achse dargestellt sind (die daher in der Anzahl den Ausgangsvariablen entsprechen werden). Durch Verbinden der Punkte entsteht eine gestufte Linie, die an einigen Stellen eine konkave Form und an anderen Stellen eine konvexe Form aufweist.
✔Wie wir aus dem Graphen erkennen können, sind auf der x-Achse die Komponenten und auf der y-Achse die Eigenwerte dargestellt.
✔Wenn die Kurve dieses Graphen einen "Ellenbogen" bildet, können wir eine Linie zeichnen und nur die Faktoren oberhalb dieser Linie berücksichtigen.
✔Aus dem hier gezeigten Graphen können wir zum Beispiel erkennen, dass die Anzahl der Punkte oberhalb des Ellenbogens 2 beträgt.
|
 |
Aufzählung
| Der letzte Teil der Hauptkomponentenanalyse besteht darin, die einzelnen gefundenen Hauptkomponenten aufzuzählen. |
 |
Durchführung einer PCA: Fallbeispiel Click to read 
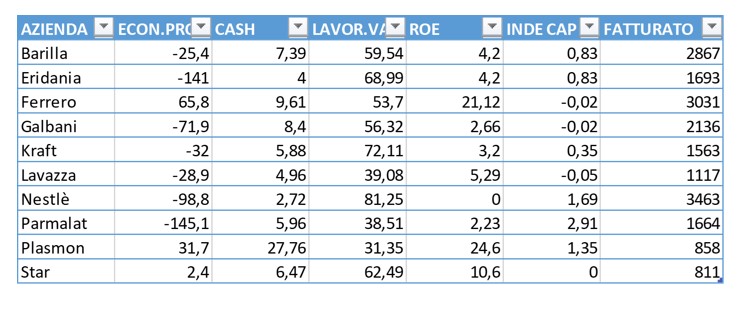
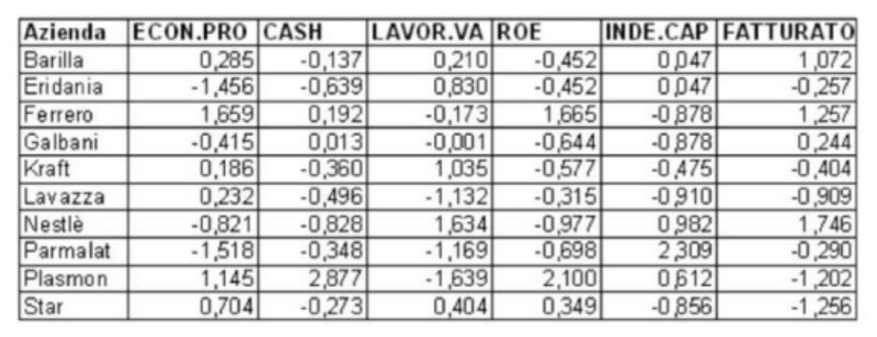
Angenommen, wir haben folgende Unternehmensleistungsumfrage zu 10 Unternehmen.
|
ECON.PRO -> Wirtschaftlicher Gewinn, Differenz zwischen der Rendite auf das investierte Kapital und dessen Kosten
CASH -> Cashflow in Prozent vom Umsatz
LAVOR.VA -> Arbeitskosten in Prozent vom Wertschöpfung
ROE -> Eigenkapitalrendite, Nettogewinn in Prozent vom Eigenkapital
INDE.CAP -> Verschuldung in Prozent vom Eigenkapital
FATTURATO: UMSATZ
|
 |
Da die Daten in sehr unterschiedlichen Einheiten ausgedrückt sind, sollten wir zur standardisierten Datenmatrix übergehen.
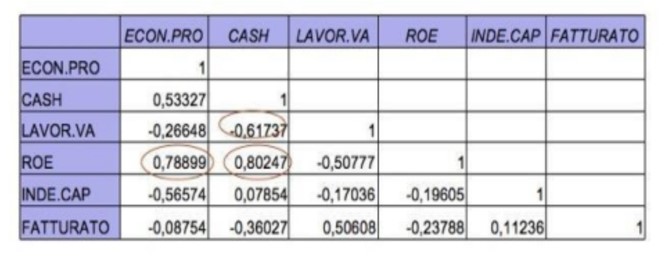
Wie bereits erwähnt, ist die Beobachtung der Korrelationsmatrix ein wichtiger Schritt: Wenn alle Variablen unkorreliert wären, gäbe es keinen Grund, mit der PCA fortzufahren, da man so viele Komponenten hätte wie beobachtete Variablen. Wenn jedoch einige Variablen stark korreliert sind, sollten wir nur eine davon in Betracht ziehen. Die Tabelle zeigt, dass ROE positiv mit dem Cash Flow und der Variable Economic Profit korreliert ist. Daher werden sie in die Analyse einbezogen.
|
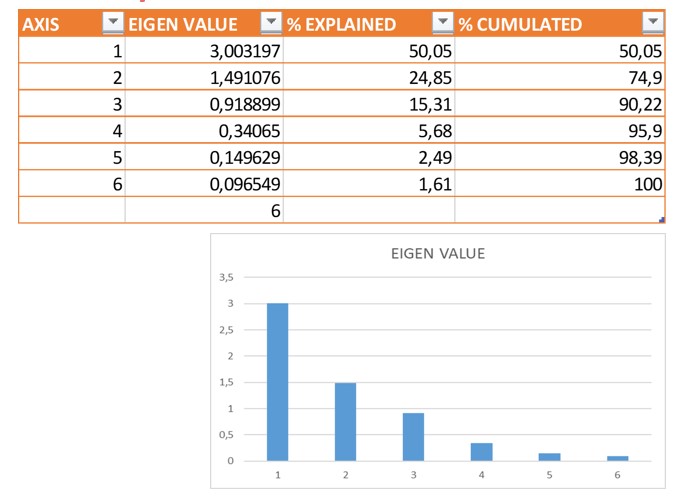
●Wir müssen Eigenwerte bzw. Eigenvektoren berechnen und den Prozentsatz der Varianz analysieren, der durch die Eigenwerte erklärt wird, indem wir das Scree-Plot verwenden.
●Eigenwerte größer als 1 erklären in diesem Fall 74,9% der ursprünglichen Varianz.
●Es ist möglich, 2 Komponenten zu extrahieren, da die ersten 2 Dimensionen eine kumulative Varianz von 75% erreichen.
|
|
|
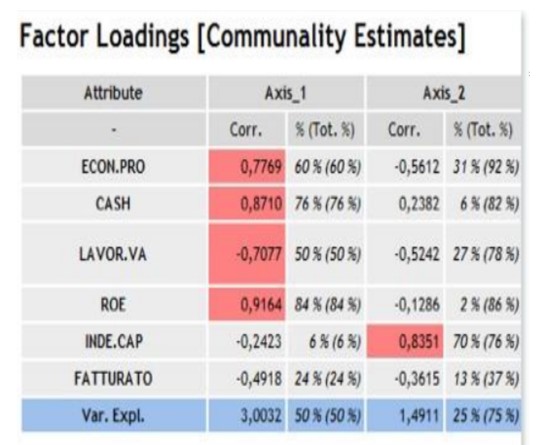
Um die Rolle jeder Variable bei der Konstruktion der Faktoren zu verstehen und somit Material zur Reflexion zu haben, um die Bedeutung der Achsen zu verstehen, können wir die Ähnlichkeit analysieren, die uns sagt, wie stark jede Variable mit der Achse korreliert ist.
Es ist zu beobachten, dass die am stärksten korrelierten Variablen diejenigen sind, die die erste Achse bestimmen. Diese Achse ist die wichtigste, da sie die maximale Variabilität zusammenfasst. Und die Menge an erklärter Variabilität wird von der Korrelation zwischen den ursprünglichen Variablen beeinflusst. Die mit der ersten Achse korrelierten Variablen legen nahe, sie als Zusammenfassung der Rentabilität (C1) zu interpretieren: auf der rechten Seite hohe Rentabilität, auf der linken Seite niedrige Rentabilität.
Die zweite Achse diskriminiert nach Verschuldung (C2): Oben befinden sich die Unternehmen mit einer hohen Verschuldungsquote, unten diejenigen mit geringerer Verschuldung.
|
 |
Wie aus dem Diagramm auf der nächsten Folie ersichtlich ist:
●Auf dem kartesischen Diagramm stellen die beiden extrahierten Hauptkomponenten die Achsen dar,
●während die Individuen (in diesem Fall die Unternehmen) auf die Ebene projiziert werden.
Sie befinden sich näher an den Faktoren, je nachdem, wie stark sie zu ihnen beigetragen haben.
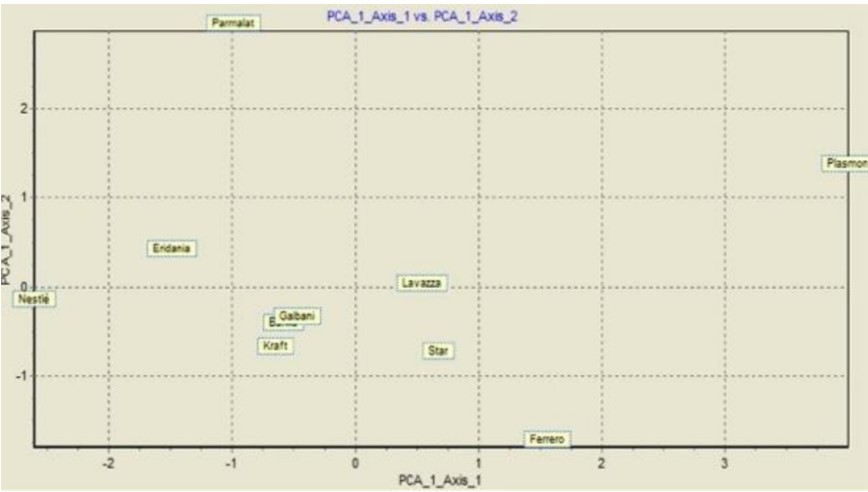
Interpretation: Einige von den Punkten befinden sich in diametral entgegengesetzten Bereichen:
●Unten rechts befindet sich Ferrero, das das gesündeste Unternehmen ist, da es eine negative Verschuldung aufweist und somit seine finanziellen Verpflichtungen mit eigenem Kapital erfüllt und eine angemessene Rentabilität aufweist.
●Im oberen rechten Quadranten finden wir Plasmon, das trotz hoher Verschuldung eine sehr hohe Rentabilität aufweist.
●Im unteren linken Quadranten befinden sich Unternehmen, die in gesättigten Märkten tätig sind und Marktführer sind. Zudem zeigen sie durch ihre Nähe zum Ursprung der Achsen, dass sie ihre finanzielle Situation im Griff haben. Durch ihre negative Verschuldung verfügen sie über Kapitalreserven, die bereit sind, um den Marktanforderungen gerecht zu werden oder um rentable Geschäftstätigkeiten zu verfolgen.
●Schließlich finden wir oben links Parmalat, das die schlechteste Situation aufweist. Es hat eine hohe Verschuldung und negative Rentabilität. Daher muss dieses Unternehmen sein Geschäftssystem unbedingt überdenken, um das Risiko der Insolvenz zu vermeiden.
Zusammenfassung
Zusammenfassung Click to read  |


























