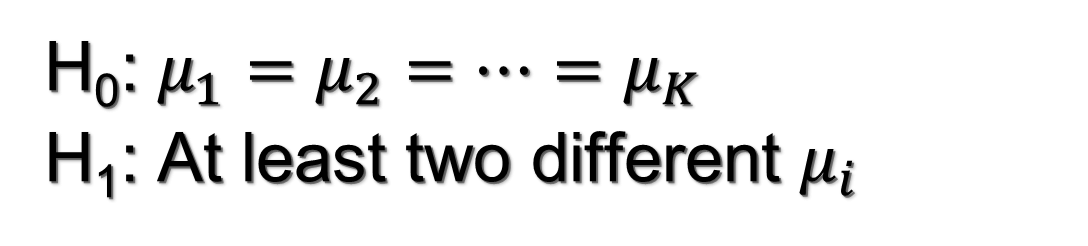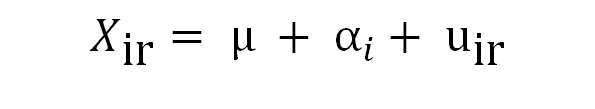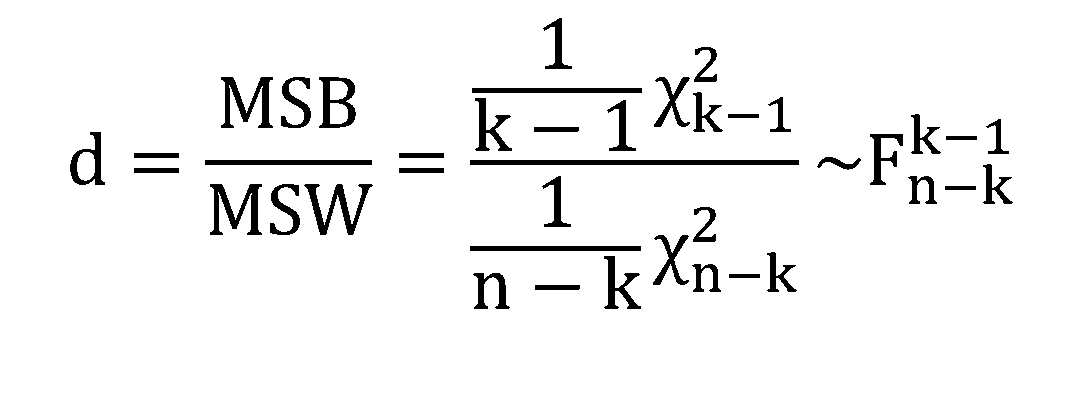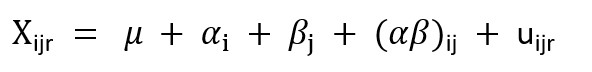Die hier vorgestellten ALM-Techniken in Form der Varianzanalyse (VA) ermöglichen die Beantwortung potenziell interessanter Fragen. Einige Beispiele:

1. Verdienen männliche und weibliche Arbeitnehmer:innen in einer Region den gleichen durchschnittlichen Jahreslohn?
2. Erhalten die Schüler:innen eines Kurses, der andere Lehrmethoden anwendet, die gleiche Durchschnittsnote?
3. Unterscheidet sich der durchschnittliche wöchentliche Verbrauch bestimmter Arzneimittel zwischen den Altersgruppen und/oder dem Geschlecht?

Die einfache VA ist für die Fragen 1 und 2 geeignet, während für Frage 3 eine zweifache VA erforderlich ist. Unser Ziel ist es, die Auswirkung einer unabhängigen Variable (Faktor), die in k verschiedene Kategorien (Niveaus) eingeteilt ist, auf eine numerische abhängige Variable (Antwortvariable) zu testen. 

Dieser Test basiert auf der Zerlegung der gesamten Stichprobenvariabilität. Wir können dieses Problem als statistischen Hypothesentest mit einer Nullhypothese (H0; unsere Standardhypothese) und einer Alternative (H1; eine alternative Hypothese) betrachten. Der Test wird in Bezug auf die Populationsmittelwerte der Zielvariablen über die Ebenen unseres Faktors (bzw. unserer Faktoren) formuliert.

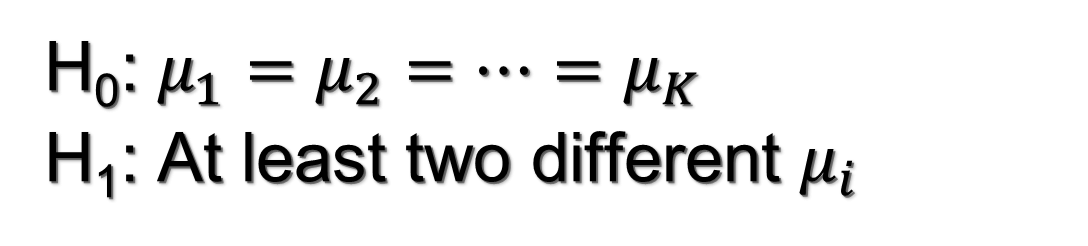
Die für die Durchführung des VA-Tests erforderlichen Annahmen sind:

• Normalverteilung: Die Verteilung der Zielvariablen auf jeder einzelnen Ebene sollte normal sein.
• Varianzgleichheit: Die Varianzen der Zielvariablen müssen auf allen Ebenen gleich sein.
• Unabhängige Stichproben: Die Stichprobendaten auf jeder Ebene des Faktors sind nicht mit den anderen Stichprobendaten (die auf den anderen Ebenen erhoben wurden) korreliert.

Das VA-Verfahren mit einem Faktor basiert auf der folgenden Gleichung:

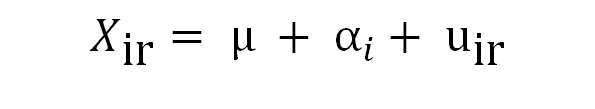
wobei 𝑋ir der Wert unserer Antwortvariable für das Individuum 𝑟 in der Kategorie (Ebene) 𝑖 ist. Wir nehmen an, dass dieser Wert die Summe von drei Effekten ist:

• Ein großer Mittelwert (μ), der für alle Individuen und Ebenen gilt
• Eine Verschiebung (α𝑖), die den mittleren Einfluss der Zugehörigkeit zur Stufe 𝑖 erfasst
• Ein Residuum (uir), das zufällige, unkontrollierte Schwankungen berücksichtigt. Es wird angenommen, dass dieses Residuum eine Normalverteilung mit einem Mittelwert von Null aufweist

Der VA-Test ist gleichbedeutend mit der Prüfung, ob die Termini α𝑖 über die k-Stufen hinweg identisch sind. Ist dies nicht der Fall, gibt es signifikante Unterschiede zwischen den Mittelwerten.
Wir nehmen Stichprobendaten zu 𝑋 und zerlegen ihre Variabilität (Streuung um die Stichprobenmittelwerte) in zwei Teile:

1. Die gruppeninterne Variabilität (SQR) ist für die interne Variabilität verantwortlich.
2. Die Zwischenvariabilität (SQA) berücksichtigt die Unterschiede zwischen dem Mittelwert der einzelnen Gruppenstichproben und dem Gesamtmittelwert.

Die Gesamtvariabilität (SQT) ist einfach die Summe von SQR+SQA. Wenn SQA viel größer ist als SQR, bedeutet dies, dass es signifikante Unterschiede in den Gruppenmittelwerten gibt. Es gibt also signifikante Unterschiede in den Mittelwerten zwischen den Ebenen des Faktors.

Um das relative Gewicht von SQA und SQR auf die Gesamtvariabilität zu vergleichen, werden sie durch die Anzahl der Freiheitsgrade geteilt, was die Werte MQA bzw. MQR ergibt. 

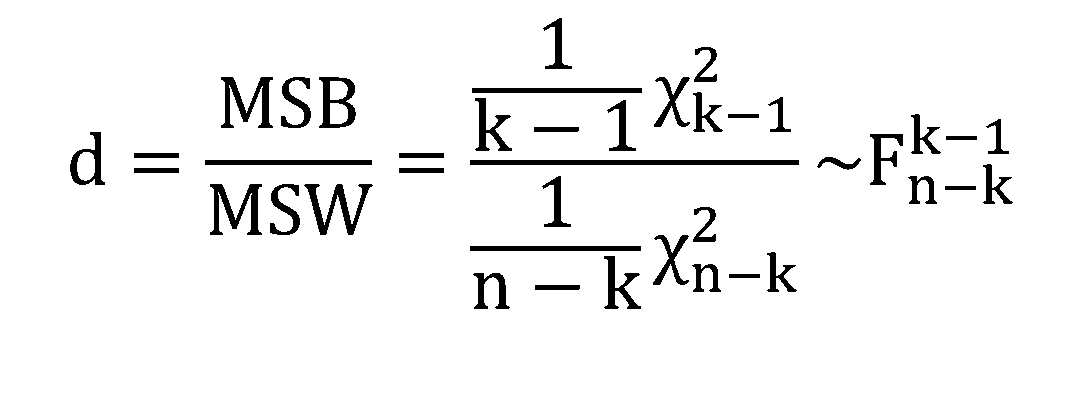
Wenn die erforderlichen Annahmen zutreffen, wird die als MQA∕MQR berechnete Statistik (d) als F-Modell verteilt. Diese Statistik ermöglicht es, eine Entscheidung über den Test zu treffen: Je höher ihr Wert ist, desto größer (relativ) ist der Zwischenanteil im Vergleich zur inneren Variabilität.
Aber wie können wir wissen, ob d hoch ist oder nicht? Durch die Berechnung des p-Wertes, der mit diesem Test verbunden ist: Wir berechnen den p-Wert (die Wahrscheinlichkeit am rechten Rand der entsprechenden F-Verteilung) und wenn dieser p-Wert niedrig ist, verwerfen wir die Nullvariante (d. h., es gibt signifikante Unterschiede im Mittelwert zwischen den Stufen).

Zur Veranschaulichung ein Beispiel: Wir wollen testen, ob das Design der Verpackungen, auf denen eine bestimmte Milchmarke verkauft wird, einen Einfluss auf den Verkauf hat. Zu diesem Zweck nehmen wir eine Stichprobe von 12 Geschäften mit ähnlichen Merkmalen, legen den gleichen Preis für die Milch fest und weisen zufällig eine Verpackungsart (1, 2 oder 3) zu. Dann erhalten wir die Stichprobendaten unserer Antwortvariable "Sales", die misst, wie viele Tausend Milchflaschen in einem Monat verkauft wurden, wie unten dargestellt: 

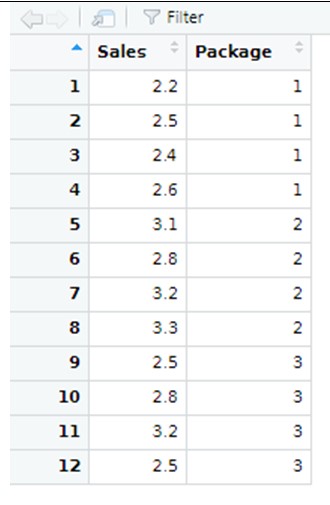
Unsere oben gezeigten Beispieldaten sind in einer R-Datei enthalten, die wir hier öffnen können (wir nennen diese Datendatei "Milk"):

Wir wollen testen, ob es statistisch signifikante Unterschiede im mittleren Umsatz gibt, abhängig von der Gestaltung des Pakets. Wir wenden VA mit R an, was die Installation bestimmter Pakete erfordert:

Um die VA anwenden zu können, müssen wir zunächst sicherstellen, dass die erforderlichen Annahmen tatsächlich zutreffen:

Diese Zeilen geben zunächst den betrachteten Datensatz an ("Milk"), gruppieren dann die Daten nach den Niveaus des Faktors ("Package") und führen schließlich einen Shapiro-Wilk-Normalitätstest für unsere Antwortvariable ("Sales") über die Gruppen hinweg durch:

Die hohen p-Werte dieses Normalitätstests für alle Ebenen erlauben es uns, unter der erforderlichen Normalitätsannahme zu arbeiten. Außerdem nehmen wir an, dass die Varianzen gleich sind, was uns dazu veranlasst, einen Barlett-Test auf homogene Varianzen durchzuführen (siehe unten):

Der unten angegebene p-Wert deutet darauf hin, dass diese Annahme sehr realistisch ist:

Da die erforderlichen Annahmen zuzutreffen scheinen, führen wir die VA-Methode durch, indem wir die folgenden Codezeilen ausführen:

Das Ergebnis ist die folgende Ausgabe:

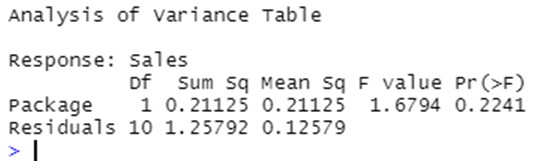
Die Ergebnisse des VA-Tests deuten darauf hin, dass die unterschiedlichen Designs der Pakete keinen Einfluss auf den mittleren Umsatz zu haben scheinen: Der Anteil der Variabilität, der durch die unterschiedlichen Niveaus des Faktors "Package" erklärt wird (Variabilität zwischen den Paketen), ist nicht signifikant größer als der restliche Anteil (innerhalb der Variationen). Folglich ist der mit diesem Test verbundene p-Wert hoch und sagt uns, dass es keinen Grund gibt, die Nullhypothese gleicher mittlerer Umsätze zwischen den Designs zu verwerfen. 

Die Ideen, die für den Fall der einfachen VA mit einem Faktor erläutert wurden, können auf Probleme ausgedehnt werden, bei denen mehr als ein Faktor unsere Antwortvariable beeinflussen kann (zweifache VA). Der VA-Test wird nun erweitert, um einen zweiten Faktor und eine mögliche Wechselwirkung zu berücksichtigen:

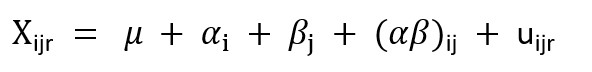
Dabei ist der Wert unserer Antwortvariable für die Person r in der Kategorie (Ebene) des Faktors und Stufe j des Faktors. Wir gehen davon aus, dass diese Werte vom großen Mittelwert abweichen (), als Summe von vier Effekten:

1. Eine Verschiebung (), die den mittleren Einfluss der Zugehörigkeit zum Niveau des Faktors umfasst 
2. Eine zweite Verschiebung (), die den mittleren Einfluss der Zugehörigkeit zum Niveau des Faktors umfasst
3. Ein Interaktionsterm zwischen diesen beiden Faktoren 
4. Ein Restwert , der zufällige, unkontrollierte Schwankungen berücksichtigt. Es wird angenommen, dass dieses Residuum eine Normalverteilung mit einem Mittelwert von Null aufweist

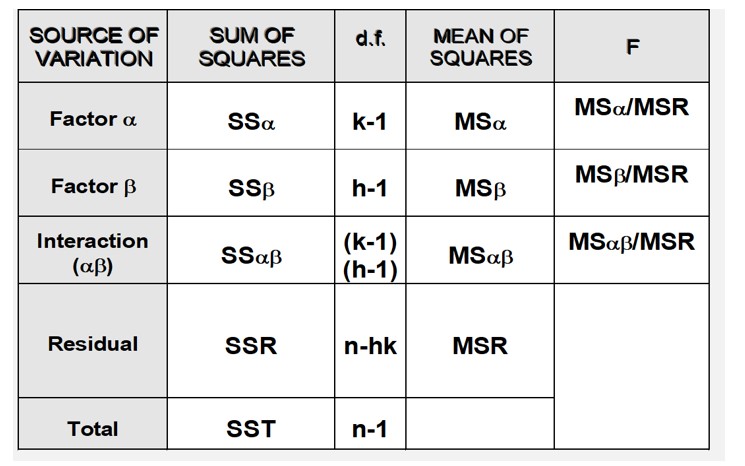
Nun sind die Vergleiche zwischen den verschiedenen Teilen der Variabilität komplexer. Jede Variationsquelle wird (praktischerweise skaliert mit der Anzahl der Freiheitsgrade) mit der Restvarianz verglichen. Die Intuition ist dieselbe wie bei der einfachen VA, aber es gibt drei verschiedene Tests, die in der folgenden Tabelle zusammengefasst sind:

Wir werden die Funktionsweise der zweifachen VA empirisch veranschaulichen und von folgendem Problem ausgehen: 
Ein Gesundheitszentrum möchte den möglichen Einfluss von Alter und Geschlecht auf die Verbrauch eines Medikaments analysieren. Zu diesem Zweck wird eine Stichprobenerhebung durchgeführt, bei der die Nutzer:innen nach Alter in vier Kategorien (Kinder, Jugendliche, Erwachsene, Senior:innen) und Geschlecht eingeteilt wurden. Es wurde eine Stichprobe von 24 Personen gezogen, wobei 3 Personen unabhängig voneinander nach Geschlecht und Altersgruppe ausgewählt wurden. Die Antwortvariable ist der monatliche Verbrauch dieses Medikaments (in €). Wir haben also den folgenden Datensatz:

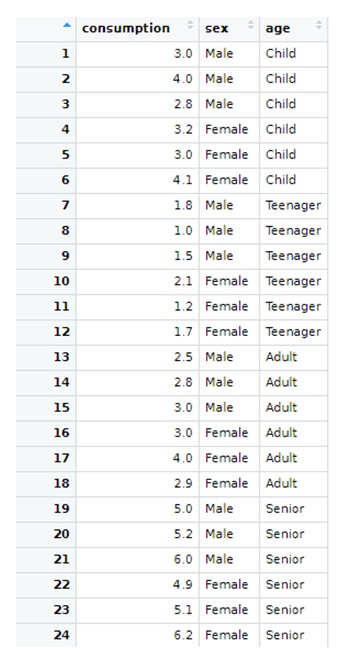
Die oben gezeigten Beispieldaten (die in einer R-Datei namens "Medicine" enthalten sind) können mit Klick auf folgendes Icon in Rstudio geladen werden:

Jetzt wenden wir eine zweifache VA (Alter und Geschlecht) mit R an, wofür bestimmte Pakete installiert und geladen werden müssen:

Um die VA anwenden zu können, prüfen wir zunächst, ob die erforderlichen Annahmen tatsächlich zutreffen, indem wir Normalitäts- und Gleichheitstests durchführen. Normalitätstests (für alle Altersgruppen und die beiden Geschlechter) werden folgendermaßen durchgeführt:

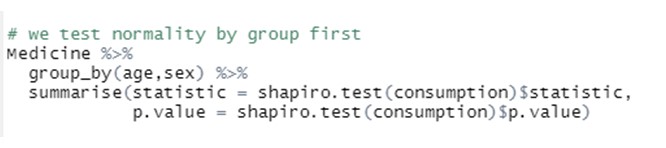
Wir geben zunächst den betrachteten Datensatz an ("medicine"), gruppieren dann die Daten nach den Niveaus der beiden in unserer Analyse berücksichtigten Faktoren ("age" und "sex") und führen schließlich einen Shapiro-Wilk-Normalitätstest für die Variable "consumption" über alle Gruppen hinweg durch:

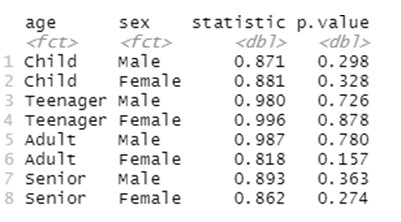
Man beachte, dass wir nun, wenn wir uns auf die Niveaus der beiden Faktoren beziehen, alle Paare von möglichen Kategorien zwischen ihnen berücksichtigen müssen. Auch hier finden wir in allen Fällen hohe p-Werte für diesen Normalitätstest, was uns erlaubt, unter der erforderlichen Normalitätsannahme zu arbeiten. Darüber hinaus sind auch homogene Varianzen erforderlich, und in diesem Fall wird diese Annahme durch die Durchführung eines Levene-Tests wie folgt geprüft:

Der gefundene p-Wert deutet darauf hin, dass wir auch in der Stichprobe keine empirischen Belege gegen diese Annahme haben:

Da die Annahmen, die für die Durchführung einer zweifachen VA erforderlich sind, zuzutreffen scheinen, führen wir die folgenden Codezeilen aus:

Das Ergebnis der Analyse liegt in Form der folgenden multiplen VA-Tabelle vor:

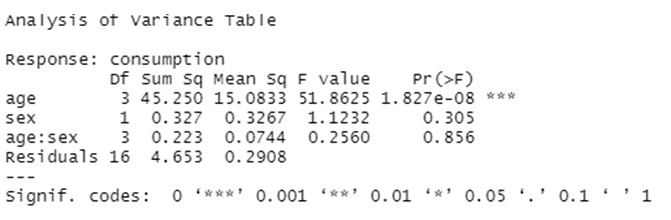
Die Ergebnisse dieser zweifachen VA liefern sehr nützliche Informationen, die eine datenbasierte Antwort auf unsere Forschungsfrage ermöglichen. Die durchgeführten Tests zeigen, dass sich die Mittelwerte des Medikamentenkonsums auf den vier Ebenen des Faktors "age" signifikant unterscheiden (dies ist der einzige Fall, in dem wir einen niedrigen p-Wert haben, der dazu führt, dass die Nullhypothese gleicher Mittelwerte verworfen wird). Wir finden jedoch weder signifikante Unterschiede im mittleren Verbrauch nach Geschlecht noch bei den Wechselwirkungen zwischen Altersgruppe und Geschlecht.