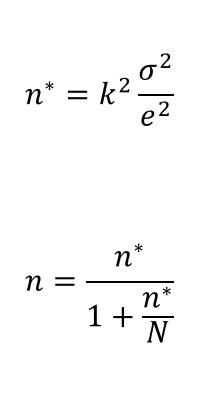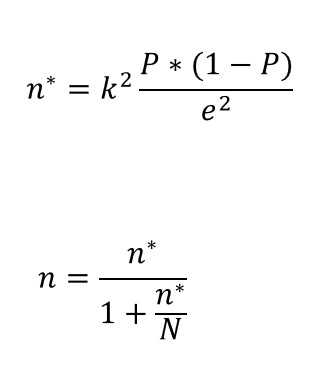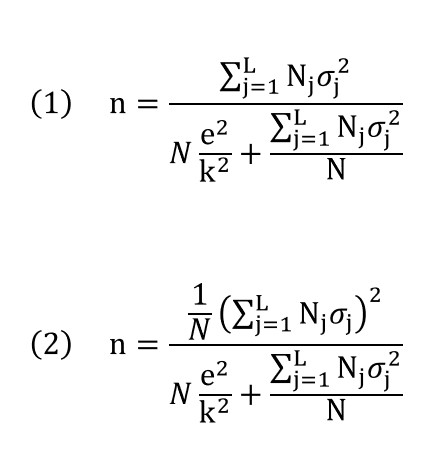|
Teoria del Campionamento
Introduzione
Introduzione Click to read 
Nell'analisi statistica, una popolazione è un set di dati per il quale vogliamo trarre alcune conclusioni.
Un sondaggio è una procedura con la quale si ottengono i dati da analizzare. I sondaggi possono essere basati sull'intera popolazione (basati sul censimento o sulla popolazione) o si potrebbe voler selezionare un sottoinsieme rappresentativo di questa popolazione. Questo sottoinsieme è definito "campione" se la sua struttura riflette la stessa struttura della popolazione e i dati raccolti dai sondaggi e trasformati in un campione sono chiamati dati campione.
Perché raccogliere set di dati sotto forma di campione invece di indagare sull'intera popolazione (indagini basate sul censimento)? Questi ultimi richiedono l'utilizzo di enormi risorse e questo si traduce in costi elevati. Al contrario, le indagini campionarie sono appropriate quando la popolazione è omogenea, poiché costituiranno una buona rappresentazione della popolazione. Inoltre, sono l'unica opzione quando la popolazione è infinita. In ogni caso, i campioni consentono di risparmiare tempo e ridurre i costi.
In termini pratici, normalmente non abbiamo le risorse per condurre studi basati sulla popolazione, quindi l'alternativa è basare la nostra analisi su campioni. Basare le nostre conclusioni su dati campione, implica che ci sarà un margine di errore intrinseco, sul quale diversi fattori possono incidere.
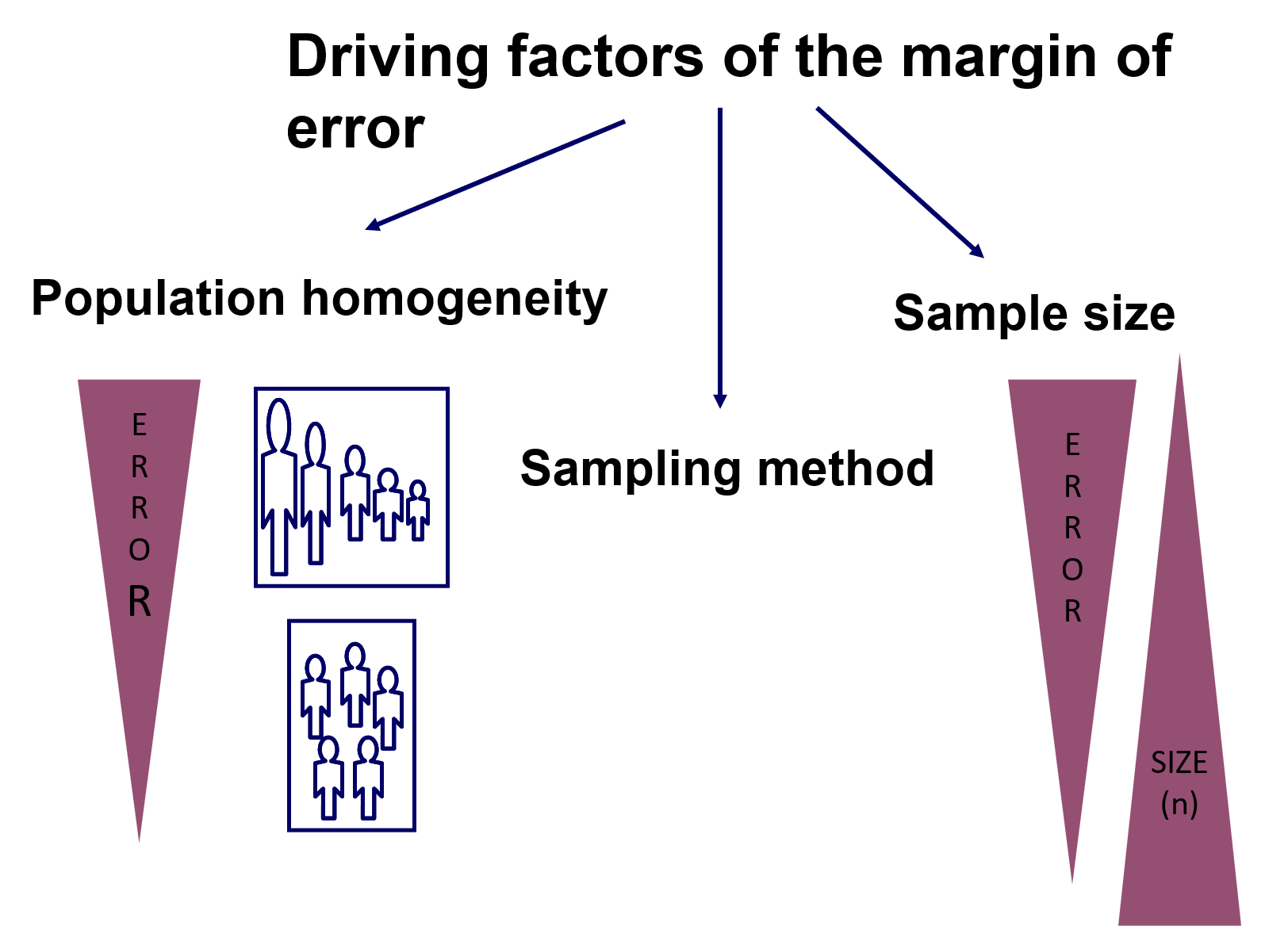
L’ errore dipenderà, fondamentalmente, da tre fattori principali:
-
Quanto sono omogenei i dati nella popolazione: più sono eterogenei, a parità di altre condizioni, maggiore è il margine di errore.
-
La dimensione del campione: più piccola è la dimensione, a parità di tutte le altre condizioni, maggiore è il margine di errore.
-
La tecnica di campionamento: a seconda delle caratteristiche dei dati.
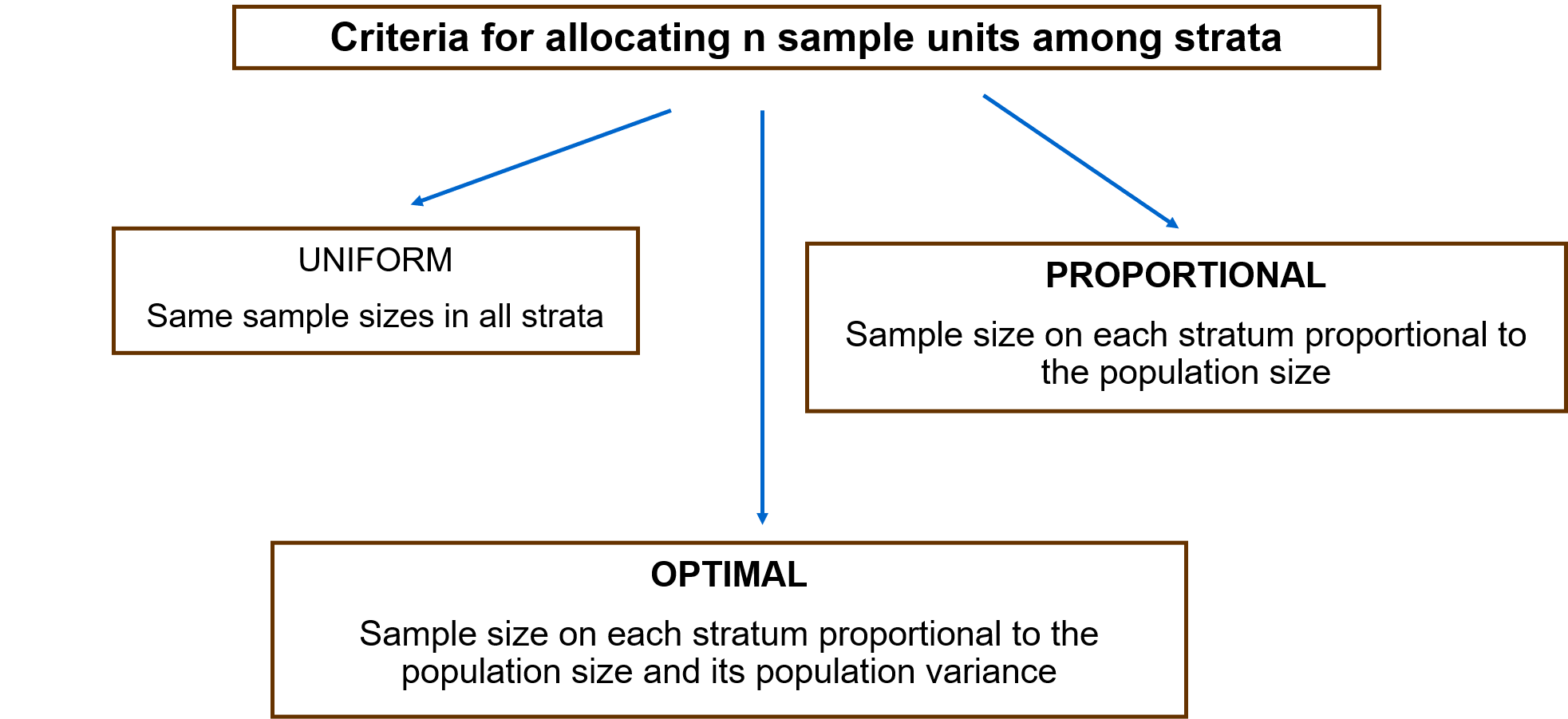
Non si può fare molto per quanto riguarda il punto a), ma c'è un certo margine di azione per punti b) e c). Per ciò che concerne il campionamento, è importante notare che è possibile applicare un'elevata varietà di tecniche di campionamento. Il diagramma seguente mostra questa varietà in termini visivi:
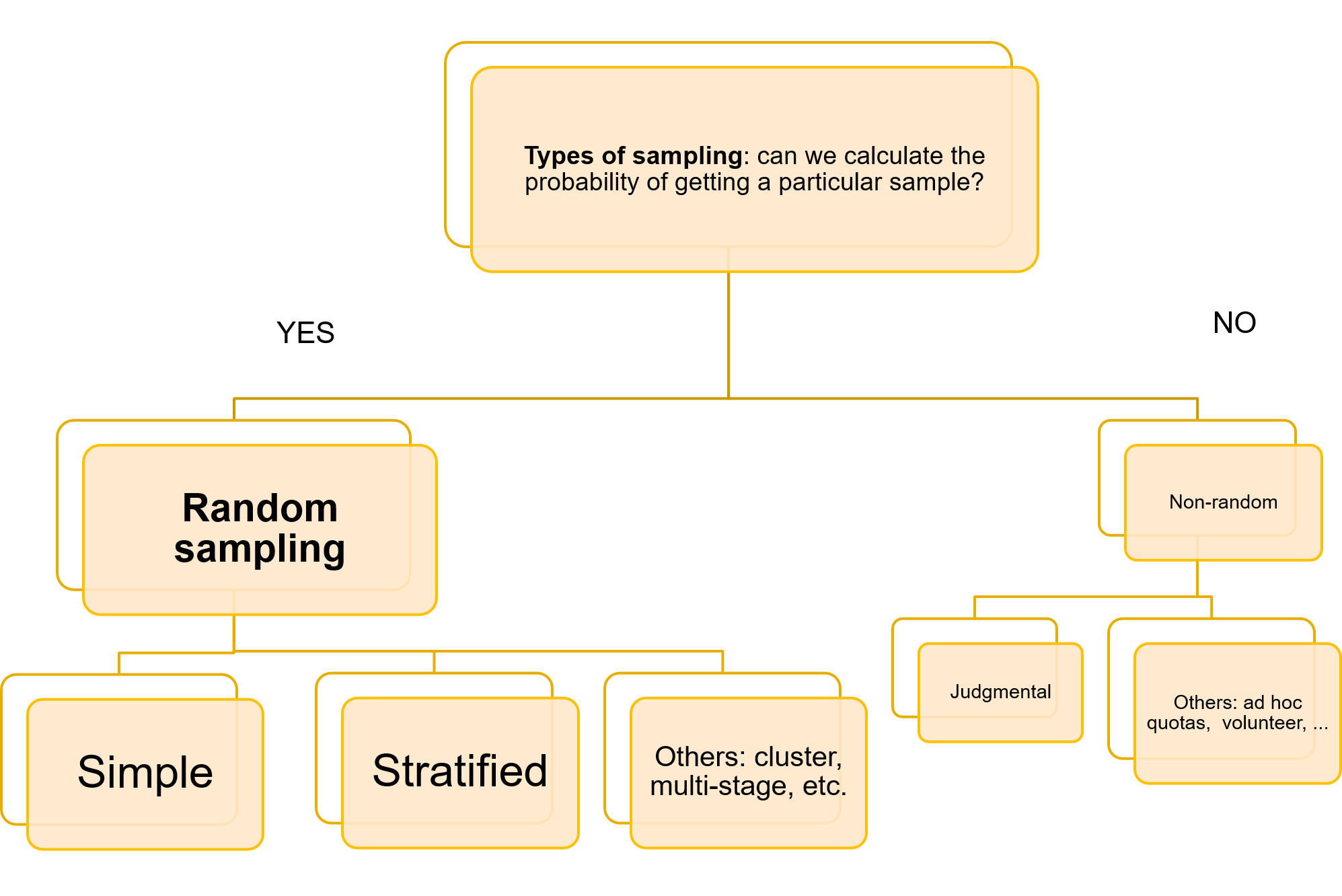
L’ errore può essere controllato solo se si lavora con campioni casuali. Le tecniche di campionamento casuale più frequentemente utilizzate sono: il campionamento casuale semplice e il campionamento casuale stratificato.
Tecniche di campionamento
Campionamento casuale semplice Click to read 
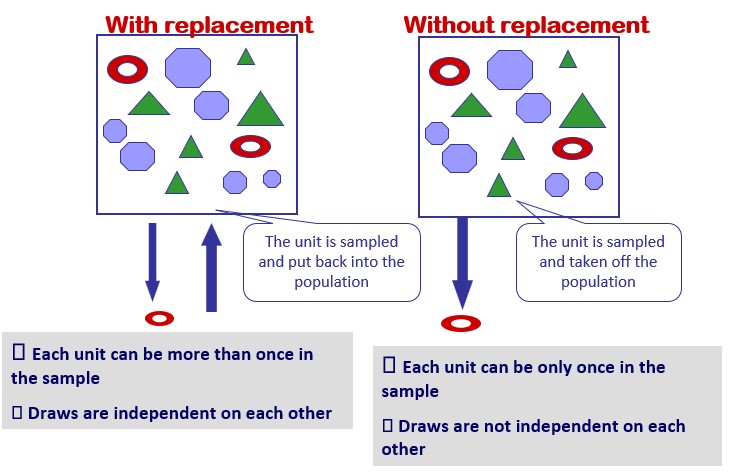
Il campionamento casuale semplice è la tecnica di campionamento più elementare che si basa sulla selezione casuale delle osservazioni esaminate. Consiste, partendo da un elenco sulle unità della popolazione, nel selezionare casualmente n di queste unità. Ma anche all'interno di questa semplice tecnica, possono essere decise alcune specifiche del processo di selezione casuale. Ad esempio, si può decidere se il campionamento avverrà con o senza sostituzione. Se il campionamento è condotto con la sostituzione, significa che ogni unità selezionata casualmente per far parte del campione viene reinserita nella popolazione dopo ogni estrazione casuale. Ciò significa che un'unità può essere campionata più di una volta, ma garantisce che le condizioni in base di ogni sorteggio siano uguali e costanti e che i risultati di ciascuna di esse siano indipendenti l'uno dall'altro.
Al contrario, se viene condotto un semplice campionamento casuale senza sostituzione, ogni unità viene campionata una sola volta, ma non possono essere garantire condizioni costanti lungo i sorteggi di selezione. Il campionamento con e senza sostituzione può produrre risultati significativamente diversi per piccole popolazioni. Sono equivalenti solo se la dimensione della popolazione (N) è molto grande.
Campionamento stratificato Click to read 
In alcune occasioni, le osservazioni sono naturalmente raggruppate in base alle caratteristiche che condividono. Ad esempio, i dati sulla distribuzione dei salari sono raggruppati in base al settore economico dei lavoratori, o al genere, o alla loro regione di residenza. I vari strati sono definiti come parti della popolazione di interesse che presentano un'elevata omogeneità interna, anche quando vi è una grande variabilità tra gli stessi. Il campionamento stratificato sfrutta questo raggruppamento delle osservazioni e seleziona casualmente un numero di unità su ogni strato L (n_L), in modo tale che la dimensione totale del campione sia ottenuta sommando gli elementi campionati su ogni strato. Esistono diversi criteri per distribuire la dimensione totale del campione tra gli strati, tra i più comuni troviamo:
- Uniforme: stessa dimensione del campione su qualsiasi strato
- Proporzionale: proporzione di membri del campione uguale alla proporzione di membri della popolazione in ogni strato
- Ottimale: proporzionale alla dimensione e all'eterogeneità (varianza) su ogni strato
Nelle stesse condizioni e con gli stessi requisiti di precisione e sicurezza, si può affermare che, in generale, il campionamento stratificato richiede una dimensione del campione inferiore rispetto al campionamento semplice. Il calcolo delle dimensioni del campione saranno dettagliate nel prossimo punto.
Calcolo delle condizioni ottimali del campione
Calcolo delle condizioni ottimali del campione Click to read 
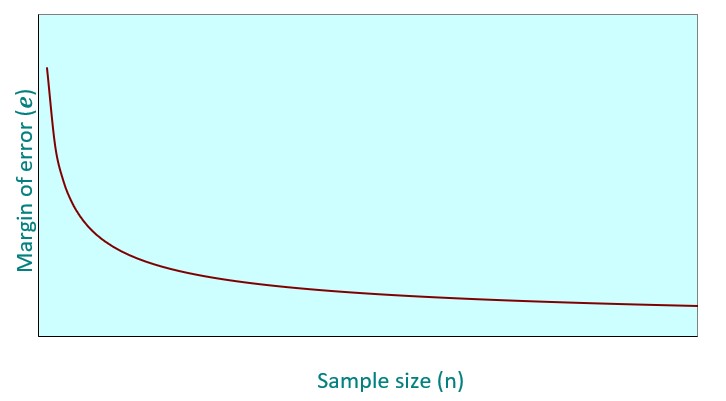
La regola d'oro in termini di correlazione tra la dimensione del campione e la precisione delle stime è che maggiore è dimensione della prima, a parità di altre condizioni, minore è il margine di errore.
Tuttavia, ottenere dati statistici, anche sotto forma di campione, può essere costoso e talvolta non si hanno le risorse per disporre di campioni di grandi dimensioni. Di conseguenza, esiste una soluzione di compromesso che stabilisce la dimensione ottimale (minima) del campione di cui si ha bisogno, dati dei requisiti in termini di precisione (margine di errore) e confidenza delle stime, e l'eterogeneità (varianza) della variabile di interesse per la popolazione.
|
Regola: maggiore è la dimensione del campione, più accurata è la stima
|
|
 |
|
Soluzione per il campionamento semplice Click to read 
Supponiamo, innanzitutto, che vogliamo che il nostro campione stimi una media della popolazione per una variabile continua e che il nostro campione venga selezionato applicando un campionamento casuale semplice. Le formule che dobbiamo applicare sono le seguenti:
Dove:
k è la costrante che deriva da una distribuzione normale e aumenta all’aumentare del livello di confidenza scelto.
e rappresenta l’errore che si è disposti ad assumere nel calcolo delle stime.
Inoltre, è necessario formulare ipotesi sull'omogeneità della variabile nella popolazione. Ciò implica che dobbiamo imporre un valore realistico (di solito proveniente da qualche studio precedente) alla varianza della popolazione σ 2.
n∗ si utilizza nel campionamento casuale semplice con sostituzione.
n invece si utilizza nel campionamento casual semplice senza sostituzione.
N è la dimensione della popolazione.
Generalmente  , con N molto grande. , con N molto grande.
Allo stesso modo, se siamo interessati a stimare la proporzione (P) di unità in una popolazione che possiede una data caratteristica, le espressioni richieste per trovare le dimensioni ottimali del campione sono:
Dove:
k, è una costante che proviene da una distribuzione normale e aumenta all’aumentare del livello di conidenza scelto.
e, è l’errore che si è disposti ad assumere del calcolo delle stime.
In questo caso, si fa un’ipotesi sul valore che deve assumere P * (1-P), che è la varianza di una variabile binaria (sì / no). Solitamente si suppone che P=1-P=0.5, quindi P*(1-P)=0.25 prenda il suo valore massimo.
Questa tecnica sarà illustrata presentando un esempio pratico su come vengono determinate le dimensioni del campione e su come l'applicazione di R.
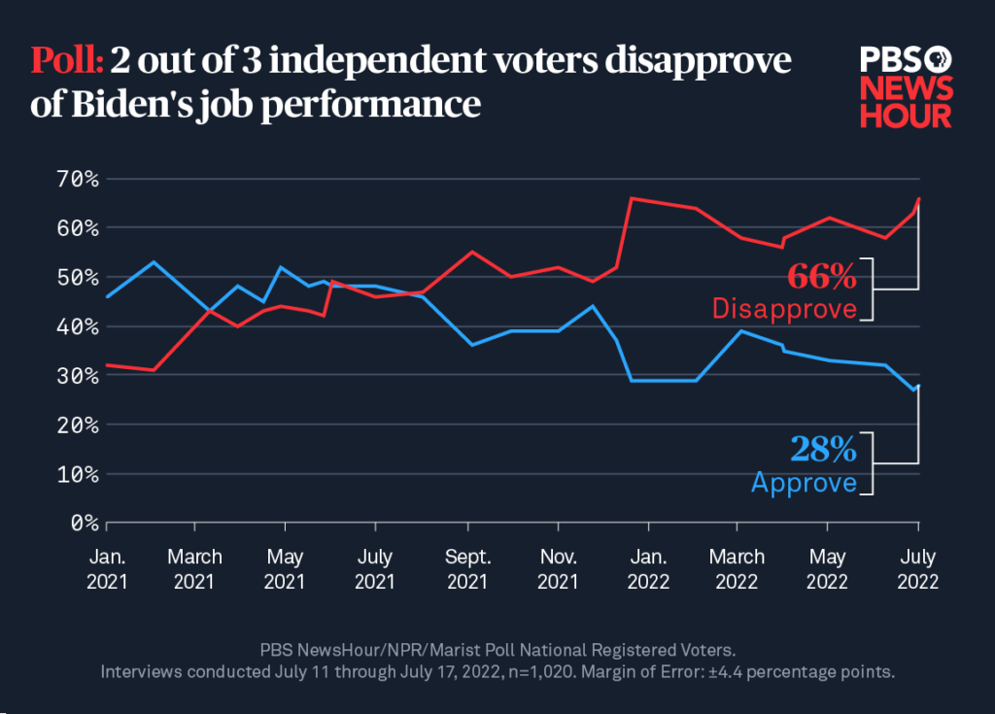
Il Public Broadcasting Service (PBS) negli Stati Uniti stima regolarmente la percentuale di cittadini che approvano o disapprovano il lavoro del presidente. Nel caso del presidente Joe Biden, questi sondaggi sono stati condotti dal gennaio 2021. Il grafico seguente mostra l'evoluzione delle stime:
In un recente sondaggio, PBS voleva ottenere stime con un livello di confidenza del 99%, accettando dunque un margine di errore del ±4,4%. Hanno ipotizzato lo scenario peggiore (soluzione usuale) e supposto che la percentuale di persone che approvano (P) sia la stessa della percentuale che non approva (1-P).
Quale sarebbe il numero di cittadini da campionare con queste condizioni? Le equazioni ripotarte in precedenza possono essere implementate in linguaggio R.
Per prima cosa è necessario installare e caricare i pacchetti richiesti:
Successivamente, si può trovare questa dimensione ottimale del campione ri-chiamando la funzione "sample.size.prop" nel pacchetto. Questa funzione consente un campionamento con o senza sostituzione, anche se da un punto di vista pratico non ci sono differenze tra i due metodi data la grande dimensione della popolazione (N) da cui vengono prelevati i campioni (possiamo arbitrariamente assumere che N = 200.000.000). Di seguito sono riportati i codici che permettono di calcolarle rispettive soluzioni per un campionamento senza e con sostituzione:
In entrambi i casi viene calcolato un campione di circa 1.000 unità.
Soluzione per campionamento stratificato Click to read 
In questo punto vengono dettagliate le formule per il calcolo delle dimensioni del campione nel caso di campionamento stratificato. Per semplicità e chiarezza, ci concentreremo solo sul caso di stima di una media della popolazione e offriremo le due soluzioni più comuni, che corrispondono ai casi di distribuzione proporzionale (1) e ottimale (2):
Come scritto in precedenza, in entrambi i casi la formula corrisponde alla stima della media della popolazione per una variabile continua con un campionamento stratificato senza sostituzione. In queste espressioni Nj sta per la dimensione dello strato j e σj2 per la varianza della variabile su questo stesso strato.
Analogamente alle soluzioni dettagliate per il campionamento casuale semplice, possiamo illustrare come le dimensioni ottimali del campione sono calcolate nel campionamento stratificato presentando un esempio pratico applicando il linguaggio R.
Supponiamo che un ente di beneficenza stia conducendo un'indagine campionaria per studiare le donazioni annuali fatte dai suoi membri, che sono classificati in tre diversi gruppi in base alla loro età con 100, 700 e 200 membri ciascuno. Da uno studio pilota questo ente di beneficenza sa che le rispettive deviazioni standard (σj) nelle donazioni annuali in ciascun gruppo sono €6, €30 e €12. Vogliamo trovare la dimensione minima del campione necessaria per stimare la donazione media annua, stabilendo un margine di errore di € 2 e un livello di confidenza del 95%.
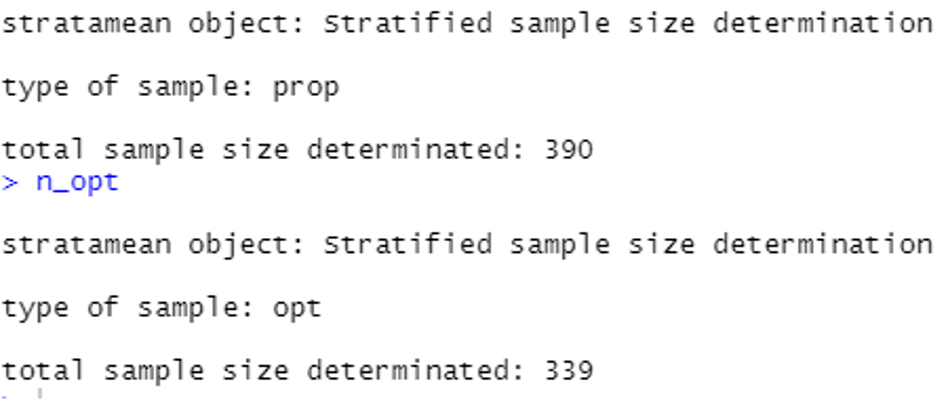
Le seguenti righe di codice calcoleranno la dimensione ottimale del campione, offrendo le soluzioni per il caso di una ripartizione proporzionale e ottimale, ri-chiamando la funzione "stratasize" inclusa nel pacchetto "samplingbook" in R:
Le rispettive soluzioni sono 390 e 339 unità, come dettagliato di seguito:
Infine, si può vedere se queste due dimensioni del campione saranno allocate tra strati. Questo si può fare utilizzando la funzione "stratasamp" nello stesso pacchetto: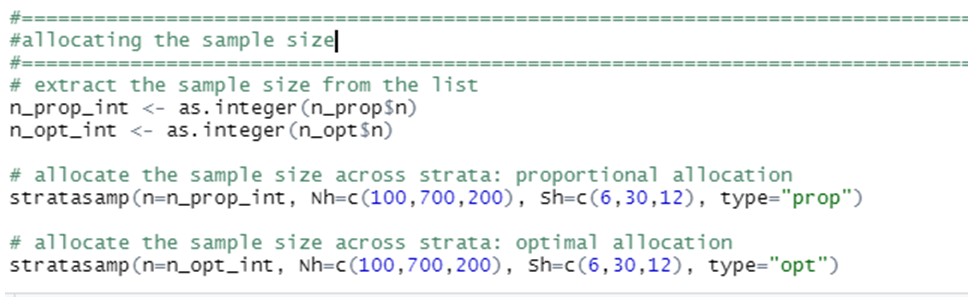
Le soluzioni sono:

|
 Riprodurre l’audio
Riprodurre l’audio