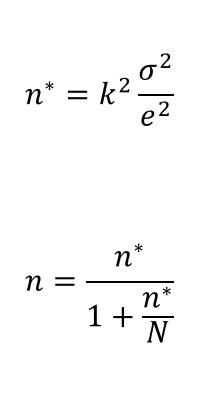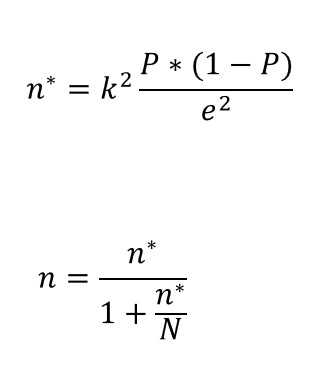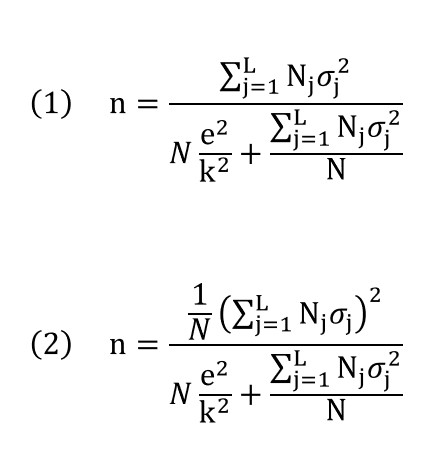|
Teoría del muestreo
Introducción
Introducción Click to read 
En el análisis estadístico una población constituye una base de datos de la que queremos extraer algunas conclusiones. Una encuesta es un procedimiento gracias al cual obtenemos datos para ser analizados. Las encuestas pueden basarse en toda la población (basadas en el censo o en la población) o basarse en un subconjunto representativo de esta población que debemos seleccionar. Este subconjunto se define como una "muestra" si su estructura refleja la misma estructura que la de la población. Los datos recopilados de las encuestas realizadas sobre una muestra se denominan datos “basados en muestras” o muestrales.
¿Por qué trabajar con bases de datos que proceden de una muestra en lugar de analizar al total de la población (encuestas basadas en censos)? Las encuestas basadas en censos son necesarias en conteos o en investigaciones de character exhaustive, pero requieren una cantidad ingente de recursos y esto se traduce en altos costes. Por el contrario, las encuestas basadas en una muestra son idóneas si la población es homogénea ya que en ese caso constituirán una buena representación de la población. Además, son la única opción cuando la población es infinita y se encuentra en procesos destructivos de información. En cualquier caso, las muestras ahorran tiempo y otros costes.
En términos prácticos, normalmente no contamos con los recursos para realizar estudios censales (poblacionales), por lo que la alternativa es basar nuestros análisis en muestras. Basar nuestras conclusiones en datos muestrales implica que habrá un margen inherente de error que va a depender de varios factores.
El margen de error dependerá, básicamente, de tres factores:
-
La homogeneidad de los datos en la población: cuanto más heterogéneos -resto constante- , mayor es el margen de error.
-
El tamaño de la muestra: cuanto menor sea el tamaño de la muestra – resto constante-, mayor será el margen de error.
-
La técnica de muestreo: que elegiremos en función de las características de los datos.
No podemos hacer mucho sobre (a), pero sí que podemos actuar sobre los factores (b) y (c). En cuanto al factor (c) y la elección de la técnica de muestreo aplicada, es importante señalar que existe una gran variedad de técnicas de muestreo disponibles que podríamos aplicar. El siguiente diagrama muestra visualmente esta variedad:
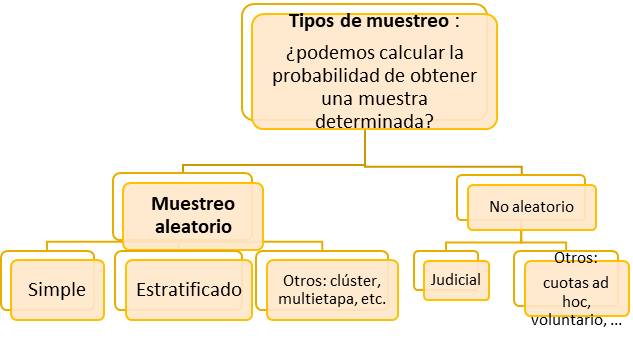
Sólo podemos controlar el margen de error de nuestras conclusiones si trabajamos con muestras aleatorias y las técnicas de muestreo aleatorio más frecuentes son el muestreo aleatorio simple y el muestreo aleatorio estratificado.
Sampling techniques
Muestreo aleatorio simple Click to read 
El muestreo aleatorio simple es la técnica de muestreo más elemental que se basa en la selección aleatoria de los individuos o unidades encuestadas. A partir de una lista de las unidades de la población, consiste en seleccionar aleatoriamente n de estas unidades. Pero incluso dentro de esta técnica simple se pueden decidir algunos detalles sobre el proceso de selección aleatoria. Por ejemplo, podemos decidir si el muestreo se va a realizar con o sin reposición. Si el muestreo se realiza con reposicion, esto significa que cada unidad seleccionada aleatoriamente para formar parte de la muestra vuelve a formar parte de la población después de cada sorteo de selección aleatoria. Esto obviamente implica que una unidad puede ser muestreada más de una vez, pero garantiza que las condiciones en las que se realiza cada sorteo de selección sean iguales y constantes, y que los resultados de cada uno de ellos sean independientes entre sí.
Por el contrario, si se realiza un muestreo aleatorio simple sin reposición, cada unidad se muestrea una sola vez, pero no podemos garantizar que las condiciones sean constantes a lo largo de los sorteos de selección. El muestreo con y sin reemplazo o reposición puede producir resultados significativamente diferentes para poblaciones pequeñas, y son equivalentes solo si el tamaño de la población (N) es muy grande.
Muestreo estratificado Click to read 
En muchas ocasiones, las observaciones se agrupan naturalmente en función de características que comparten. Por ejemplo, los datos sobre la distribución de los salarios se agrupan según el sector económico de los trabajadores, su género o su región de residencia. Los estratos se definen como partes de la población de interés que presentan una alta homogeneidad interna, aun cuando existe una gran variabilidad entre estratos. El muestreo estratificado aprovecha esta agrupación de las observaciones y selecciona aleatoriamente un número de unidades en cada estrato L ( nL ), de modo que el tamaño total de la muestra se obtiene sumando los elementos muestreados en cada estrato. Existen varios criterios para asignar el tamaño total de la muestra entre estratos, siendo los más comunes los siguientes:
- Uniforme: mismo tamaño de muestra en cualquier estrato
- Proporcional: proporción de miembros de la muestra igual a la proporción de miembros de la población en cada estrato
- Óptimo: proporcional al tamaño y heterogeneidad (varianza) en cada estrato
En las mismas condiciones y con los mismos requisitos de precisión y confianza, podemos afirmar que, en términos generales, el muestreo estratificado requiere un tamaño de muestra más pequeño que el muestreo simple, pero las cuestiones relacionadas con el cálculo de tamaños de muestra se detallarán en el siguiente punto.
Cálculo de tamaños óptimos de muestras
Cálculo de tamaños óptimos de muestras Click to read 
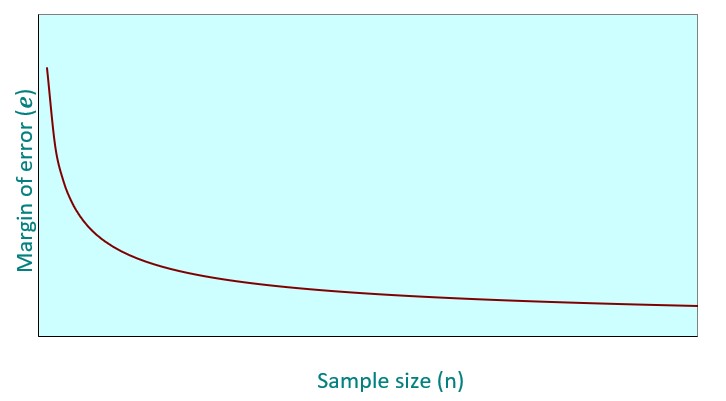
La regla de oro en términos de relacionar el tamaño de la muestra con la precisión de nuestras estimaciones es que cuanto mayor sea el tamaño – resto constante-, menor será el margen de error. Sin embargo, generar datos estadísticos, incluso si es en forma de muestra, puede ser costoso y, a veces, no tenemos recursos para tener muestras grandes. Como consecuencia, existe una solución de compromiso que establece el tamaño de muestra óptimo (mínimo) que necesitamos, dados nuestros requisitos en términos de precisión (margen de error) y confianza de nuestras estimaciones, y la heterogeneidad (varianza) de la variable de interés en la población.
|
Regla: cuanto mayor sea el tamaño de la muestra, más precisa será la estimación
|
|
 |
|
Solución para muestreo simple Click to read 
Supongamos primero que queremos que nuestra muestra estime una media poblacional para una variable continua, y nuestra muestra se seleccionará aplicando un muestreo aleatorio simple. Las fórmulas que debemos aplicar son las siguientes:
La constante k proviene de una distribución normal y aumenta si aumentamos el nivel de confianza deseado y el símbolo e representa el margen de error que estamos dispuestos a asumir. Además, necesitamos hacer una suposición sobre la homogeneidad de la variable en la población. Esto implica que debemos imponer un valor realista (generalmente proveniente de algún estudio previo) sobre la varianza poblacional σ 2.
En estas ecuaciones, n∗ es la solución para un muestreo aleatorio simple con reemplazo, n es la solución para un muestreo aleatorio simple sin reemplazo y N es el tamaño de la población. En términos generales  , y ambas soluciones convergen cuando N es muy grande. , y ambas soluciones convergen cuando N es muy grande.
De manera similar, si estamos interesados en estimar la proporción (P) de unidades en una población que tienen una característica dada, las expresiones requeridas para encontrar tamaños de muestra óptimos en esta técnica de muestreo son:
Nuevamente, la constante k proviene de una distribución normal y aumenta si aumentamos el nivel de confianza deseado, y el término e representa el margen de error que estamos dispuestos a asumir. En este caso, necesitamos hacer una suposición sobre el valor de P*(1-P), que es la varianza de una variable binaria (sí/no). La solución habitual es suponer P= 1 - P= 0.5, por lo que P* ( 1 – P ) = 0.25 toma su valor máximo.
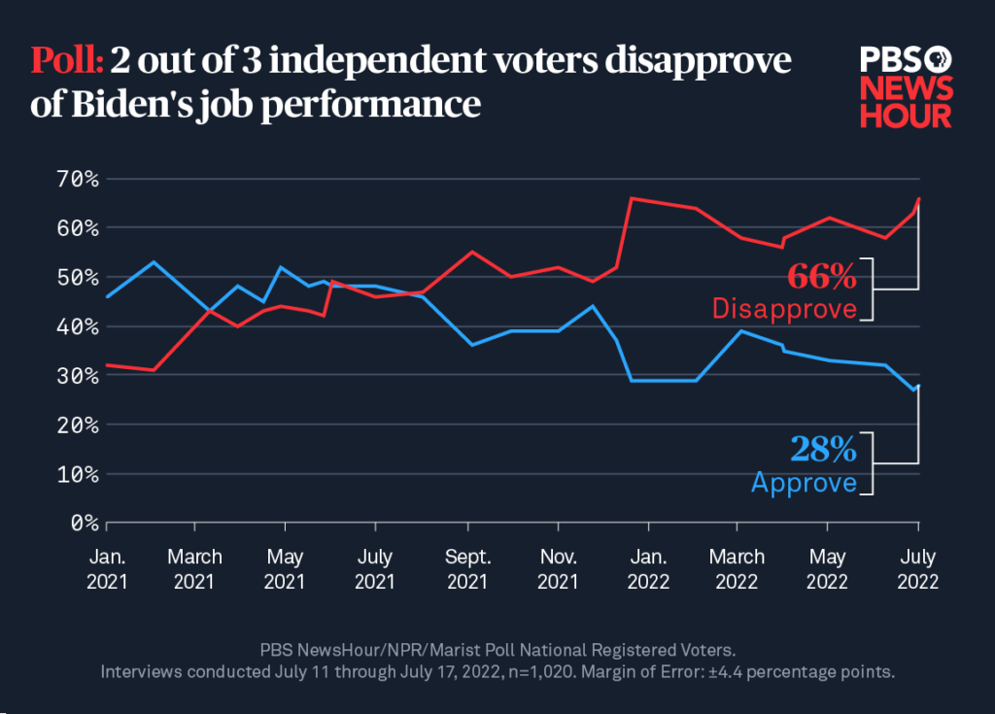
Podemos ilustrar esta técnica presentando un ejemplo práctico sobre cómo se determinan los tamaños de muestra y cómo la aplicación de R puede ayudarnos en este sentido: el Public Broadcasting Service (PBS) en EE.UU. estima regularmente el porcentaje de ciudadanos que aprueban o desaprueban la gestión del president. En el caso del Presidente Joe Biden, PBS lleva realizando estas encuestas desde enero de 2021. El siguiente gráfico muestra la evolución de sus estimaciones:
En una encuesta reciente a lo largo de esta serie, PBS quería tener estimaciones con un nivel de confianza del 99 %, estaban dispuestos a tener un margen de error de ±4,4 % y asumieron el peor de los casos (solución habitual) y supusieron que el porcentaje de personas que aprueban la gestión de Biden (P) es el mismo que el porcentaje que no la aprueba (1 – P ). ¿Cuál sería el número de ciudadanos a muestrear con estas condiciones? Las ecuaciones que se muestran arriba se pueden implementar en lenguaje R para encontrar una solución.
Primero necesitamos instalar y cargar los paquetes requeridos:
Y luego, podemos encontrar este tamaño de muestra óptimo llamando a la función " sample.size.prop " en el paquete “samplingbook”. Esta función permite un muestreo con o sin reposición, aunque no se encontrarán diferencias prácticas entre la solución de estas dos alternativas dado el gran tamaño de población (N) de la que se extraen las muestras (podemos suponer arbitrariamente que N=200.000.000). Las siguientes piezas de código calculan las soluciones respectivas para un muestreo sin y con reemplazo:
En ambos casos la solución al tamaño de muestra óptimo es aproximadamente 1.000 unidades.
Solución para muestreo estratificado Click to read 
En este punto se detallan las fórmulas para el cálculo de tamaños (óptimos) de muestra en el caso de muestreo estratificado. En aras de la sencillez y claridad, nos centraremos únicamente en el caso de estimar una media poblacional, y ofreceremos las dos soluciones más habituales, que corresponden a los casos de asignación por criterio proporcional (1) y criterio óptimo (2):
Como se ha comentado anteriormente, en ambos casos la fórmula corresponde a la estimación de la media poblacional para una variable continua con un muestreo estratificado sin reposición. En estas expresiones Nj representa el tamaño del estrato j y σj2 la varianza de la variable en este mismo estrato.
De manera similar a las soluciones detalladas para el muestreo aleatorio simple, podemos ilustrar cómo se calculan los tamaños de muestra óptimos en el muestreo estratificado presentando un ejemplo práctico aplicando el lenguaje R.
Supongamos que una organización benéfica está realizando una encuesta por muestreo para estudiar las donaciones anuales realizadas por sus miembros, que se clasifican en tres grupos diferentes según su edad con 100, 700 y 200 miembros cada uno. A partir de un estudio piloto, esta organización benéfica sabe que las respectivas desviaciones estándar (σj) en las donaciones anuales en cada grupo son 6€, 30€ y 12€. Queremos encontrar el tamaño de muestra mínimo necesario para estimar la donación media anual, estableciendo un margen de error de 2€ y un nivel de confianza del 95%.
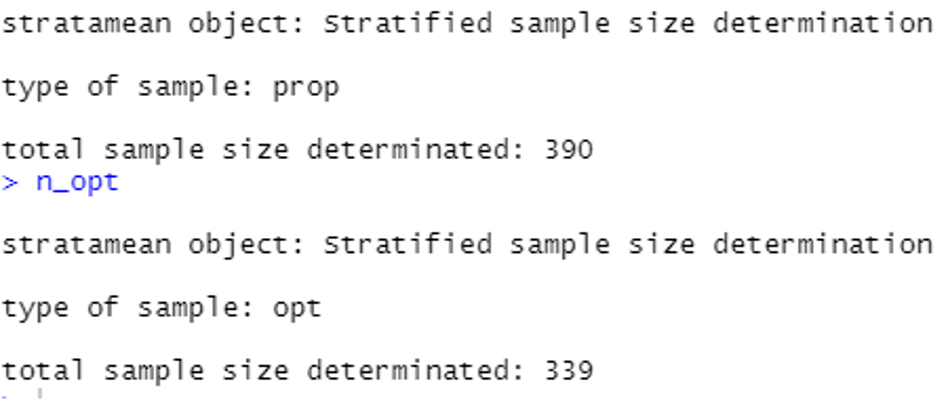
Con la función " stratasize " incluida en el paquete " sampleingbook " de R, podremos calcular el tamaño (óptimo) de la muestra y las soluciones para el caso de una asignación bajo el criterio proporcional y bajo el criterio óptimo,:
Las soluciones respectivas son 390 y 339 unidades, como se detalla a continuación:
Finalmente, podemos preguntarnos cómo se asignarán estos dos tamaños de muestra entre los estratos. Esto se puede hacer con la función " stratasamp " de este mismo paquete:
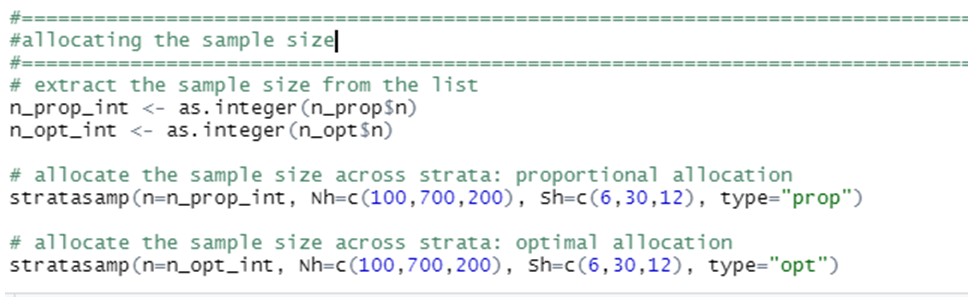
Siendo las soluciones:

|
 Reproducir el audio
Reproducir el audio