|
Analiza Componentelor Principale (ACP)
Introducere
Introducere Click to read 
Obiective
Obiectivul acestui modul este de a introduce ?i explica tehnica Analizei Componentelor Principale.
La finalul acestui modul, vei fi capabil s?:
?Cuno?ti logica ACP;
?Cuno?ti criteriile;
?Realizezi o ACP.
Defini?ie
? Analiza componentelor principale (ACP) este o tehnic? statistic? de analiz? multivariat? pentru reducerea dimensionalit??ii. În practic?, este utilizat? pentru seturile de date care con?in multe variabile corelate între ele ?i se dore?te reducerea num?rului acestora cu pierderea a cât mai pu?in? informa?ie
? ACP are obiectivul de a maximiza varian?a, calculând ponderea atribuit? fiec?rei variabile la start pentru a le putea concentra într-una sau mai multe variabile noi (denumite componente principale) care vor fi combina?ii liniare ale variabilelor de start
ACP în via?a real?
? ?tiin?ele sociale se confrunt? adesea cu cercet?ri care abund? de indicatori utiliza?i pentru a în?elege mai bine fenomenul studiat
? Un exemplu de situa?ie în care poate fi utilizat? ACP poate fi evalu?rile studen?ilor pentru un anumit curs, pe baza a mai multor variabile. Adesea, un num?r mare de variabile este utilizat pentru a evalua gradul de satisfac?ie al unui curs, cum ar fi evaluarea manualelor, a materialelor suport folosite, gradul de comfort în s?lile de clase, orarul, num?rul de ore de tutoring, etc. ACP va reduce dimensionalitatea ?i va simplifica analiza.
Cerin?ele ACP
Cerin?ele Analizei Componentelor Principale Click to read 
Variable Analysis
|
Pentru a în?elege dac? are sens s? se efectueze o analiz? a componentelor principale, este important s? fie analizate variabilele utilizate pentru a avea o imagine clar? asupra caracteristicilor lor. Mai exact, variabilele trebuie s? îndeplinieasc? urm?toarele condi?ii:
|
 |
Variabilele trebuie s? fie cantitative
|
?ACP este valid? doar dac? variabilele sunt numerice.
?În cazul în care unit??ile de m?sur? sunt diferite, variabilele trebuie standardizate înainte de a efectua procedura.
Totu?i, în unele cazuri tehnica este aplicat? si pentru variabile m?surate pe scala ”Likert” ?i pentru variabile binare. De?i din punct de vedere numeric rezultatele sunt foarte asem?n?toare, în aceste cazuri ar fi de preferat utilizarea unor metode alternative
|
 |
- Trebuie s? existe o corela?ie liniar? între variabile
?Prima etap? care trebuie parcurs? atunci când este realizat? ACP este calculul matricii de varian??/covarian?? sau a matricii de corela?ie Pearson.
?ACP este de fapt o tehnic? care poate fi aplicat? atunci când ipotezele coeficientului de corela?ie liniar? Pearson sunt respectate.
- Lipsa valorilor extreme (outlier-ilor
|
? A?a cum este cazul pentru toate analizele bazate pe varian??, valorile extreme pot influen?a rezultatele analizei, în special dac? valorile extreme sunt foarte mari ?i e?antionul este de dimensiuni mici.
? În acest sens, este util? crearea de box-plot-uri ?i de scatter-plot-uri, din care este posibil? deducerea rela?iilor liniare dintre perechi de variabile.
|
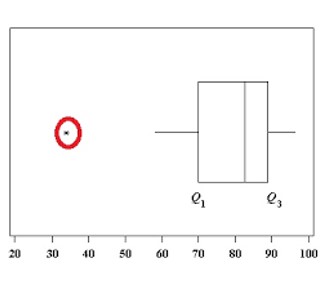 |
Dimensiunea suficient de mare a e?antionului
|
?Nu exist? o valoare prag unic?, dar în general este recomandat s? exist? cel pu?in 5-10 unit??i statistice pentru fiecare variabil? care se dore?te a fi inclus? în ACP.
?De exemplu, dac? se încearc? sistematizarea a 10 variabile în componente noi, ar fi de dorit ca e?antionul s? aib? cel pu?in 150 de observa?ii.
|
 |
Cum se realizeaz? ACP
Cum se realizeaz? ACP Click to read 
- Verificarea gradului de adecvare a e?antionului
Pentru a verifica dac? e?antionul este adecvat pentru ACP, se pot efectua anumite teste, cum ar fi:
? Testul Kaiser-Meyer-Olkin (KMO), care stabile?te dac? variabilele considerate sunt consistente pentru a putea fi utilizate în analiza componentelor principale. Indicele ia valori înre 0 ?i 1, iar pentru a face sens într-o analiz? a componentelor principale, trebuie s? aib? o valoare mai mare de 0.5.
? Testul de sfericitate Bartlett: este un test de testare a ipotezei statistice, având drept ipotez? nul? c? matricea de corela?ie coincide cu matricea identitate. Dac? acesta este cazul, nu are sens s? fie realizat? ACP, întrucât ar însemna c? variabilele nu sunt deloc corelate liniar între ele.
- Extragerea componentelor principale
|
Pentru a în?elege mai bine conceptul, s? ne imagin?m c? setul de date este ca un ora? necunoscut!
Fiecare component? principal? este o strad? în acest ora?. Dac? am vrea s? cunoa?tem ora?ul, câte str?zi am vizita? Am începe probabil cu strada central? (prima component? principal?) ?i apoi am explora celelalte str?zi.
Cât de multe str?zi ar trebui s? explor?m?
|
|
Pentru a putea spune c? am ajuns c? cunoa?tem suficient de bine ora?ul, num?rul de str?zi variaz? în func?ie de m?rimea ora?ului ?i cât de similare sau de diferite sunt str?zile.
În mod similar, num?rul de componente care vor fi extrase depinde de num?rul de variabile care sunt incluse în analiza componentelor principale ?i cât de similare sunt acestea între ele.
De fapt, cu cât sunt mai corelate, cu atât este mai sc?zut num?rul de componente principale necesare pentru a ob?ine o imagine cât mai fidel? a variabilelor de start. Din contr?, dac? gradul de corelare dintre ele este sc?zut, va trebui extras un num?r mai mare de componente principale pentru a avea informa?ii cât mai precise pentru setul de date.
Cum se realizeaz? ACP: Criteriile Click to read 
- Valori proprii mai mari de 1
|
Conform acestei reguli, se vor alege componentele care au asociat? o valoare proprie mai mare de 1.
Valoarea proprie este un num?r care arat? varian?a explicat? de component?: întrucât ini?ial varian?a explicat? de fiecare variabil? este egal? cu 1, nu ar face sens s? fie aleas? o component? (care este o combina?ie de variabile) cu varian?a mai mic? de 1.
|
 |
- Propor?ia din varian?a total? explicat?
Pe baza acestui criteriu, se p?streaz? componentele principale care explic? cumulat cel pu?in 70% din varian?a total?.
Mai mult, fiecare component? extras? ar trebui s? aduc? o cre?tere semnificativ? în varian?a de ansamblu (de exemplu, cel pu?in 5% sau 10% mai mult la variabilitatea explicat?).
- Scree Plot
|
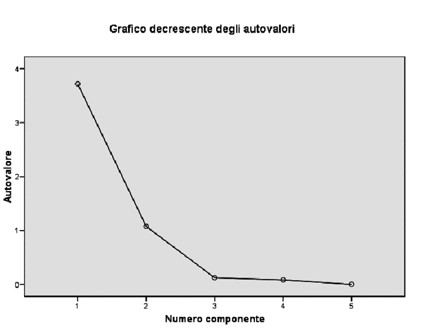
Aceast? metod? se bazeaz? pe un grafic în care valorile proprii sunt afi?ate pe axa vertical? ?i toate componentele posibil a fi extrase sunt pe axa orizontal? (care va fi deci egal? ca num?r cu cel al variabilelor de start). Prin unirea punctelor se va ob?ine o linie frânt? care în unele p?r?i va avea o form? concav?, iar în alte p?r?i o form? convex?.
? Dup? cum se poate observa din grafic, componentele sunt afi?ate pe axa Ox, în timp ce valorile proprii sunt pe axa O
? Când curba de pe acest grafic formeaz? un "elbow" (o cotitur?), este momentul tras?rii unei linii si se vor lua în considerare numai factorii care se situeaz? deasupra.
? Din graficul de mai sus, de exemplu, se poate observa c? num?rul de puncte deasupra ”elbow” (cotiturii) este 2.
|
 |
- Numirea Componentelor
| Ultima parte a ACP const? în atribuirea unor nume componentelor principale g?site. |
 |
Cum se realizeaz? ACP: Studiu de caz Click to read 
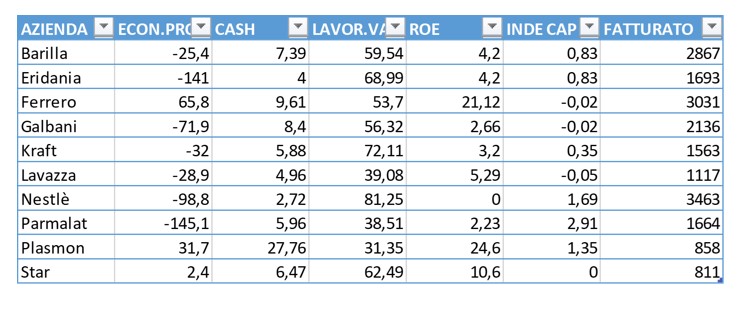
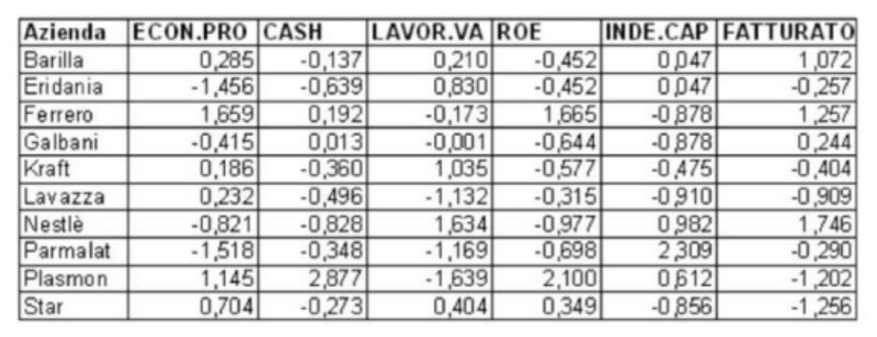
S? presupunem c? avem urm?toarele informa?ii dintr-un sondaj privind performan?a a 10 companii
|
ECON.PRO -> profitul economic, diferen?a dintre randamentul capitalului investit ?i costul acestuia
CASH -> cash-flow la cifra de afaceri în %
LAVOR.VA -> costul cu factorul munc? pe valoare ad?ugat?, în %
ROE -> randamentul capitalului propriu, profit net pe capitaluri proprii, în %
INDE.CAP -> datorii pe capitaluri propri
FATTURATO: Cifra de afaceri
|
 |
Întrucât datele sunt exprimate în unit??i de m?sur? diferite, vom utiliza matricea de date standardizat?
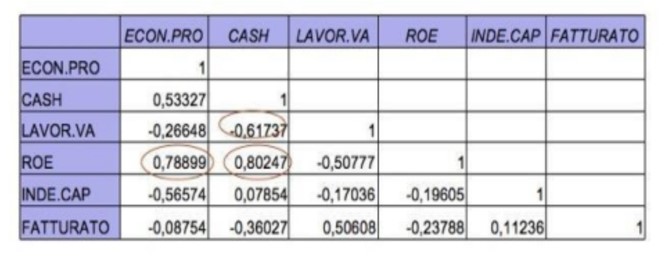
Dup? cum am men?ionat deja, observarea matricii de corela?ie reprezint? o etap? important?: dac? toate variabilele ar fi necorelate, nu ar exista motive pentru a continua cu ACP, întrucât ar fi la fel de multe componente ca variabilele observate. Dac?, din contr?, unele variabile sunt puternic corelate, ar trebui s? lu?m în calcul doar una. Tabelul de mai jos arat? c? ROE este corelat? pozitiv cu variabilele Cash-Flow ?i Profit Economic, dar le lu?m în calcul în analiz?.
|
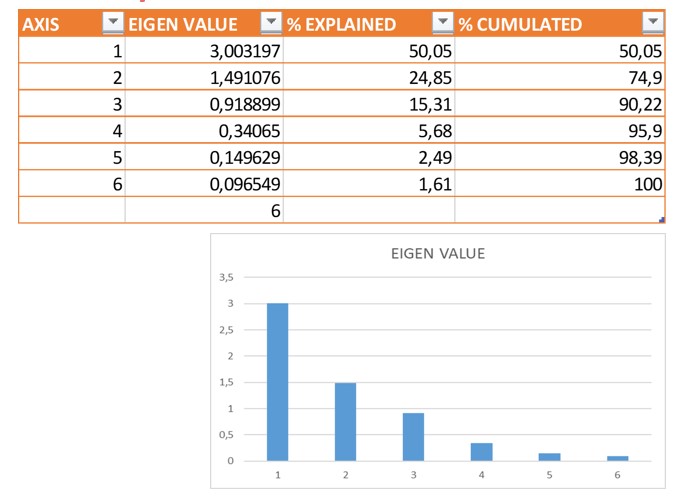
? Trebuie s? calcul?m valorile proprii, vectorii proprii, analiz?m propor?ia din varian?a explicat? de valorile proprii cu ajutorul screeplot.
?În acest caz, valorile proprii mai mari de 1 explic? 74.9% din varian?a ini?ial?
?Se pot extrage 2 Componente, ?inând cont c? primele dou? dimensiuni preiau 75% din varian?a cumulat?.
|
|
|
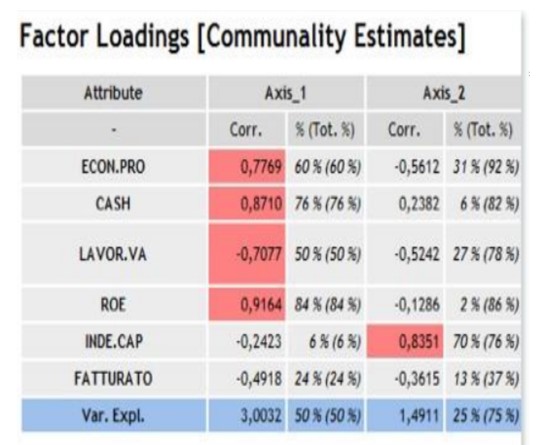
Pentru a în?elege rolul jucat de fiecare variabil? în construirea factorilor, ?i deci pentru a avea suportul necesar pentru a întelege semnifica?ia axelor, putem analiza comunalit??ile, care ne spun cât de mult este corelat? fiecare variabil? cu axa.
Se poate observa c? variabilele care sunt cel mai corelate sunt cele care determin? prima ax?. Aceast? ax? este cea mai important? deoarece este cea care sintetizeaz? variabilitatea maxim?. Cantitatea de variabilitate explicat? este influen?at? de gradul de corelare dintre variabilele originale.
Variabilele corelate cu prima ax? sugereaz? c? aceasta poate fi interpretat? ca un sumar al profitabilit??ii (C1): în partea dreapt? este profitabilitatea ridicat?, în partea stâng? profitabilitatea sc?zut?.
A doua ax? distinge prin prisma îndator?rii (C2): în partea de sus sunt companiile cu o rat? ridicat? de îndatorare, în partea de jos cele mai pu?in îndatorate.
|
 |
Dup? cum se poate observa din graficul de pe slide-ul urm?tor
? În plan Cartezian, cele dou? componente principale extrase reprezint? axel
? Unit??ile (în acest caz, companiile) sunt proiectate pe pla
? Companiile sunt situate mai aproape de factori, în func?ie de cât de mult au contribuit la ace?tia.
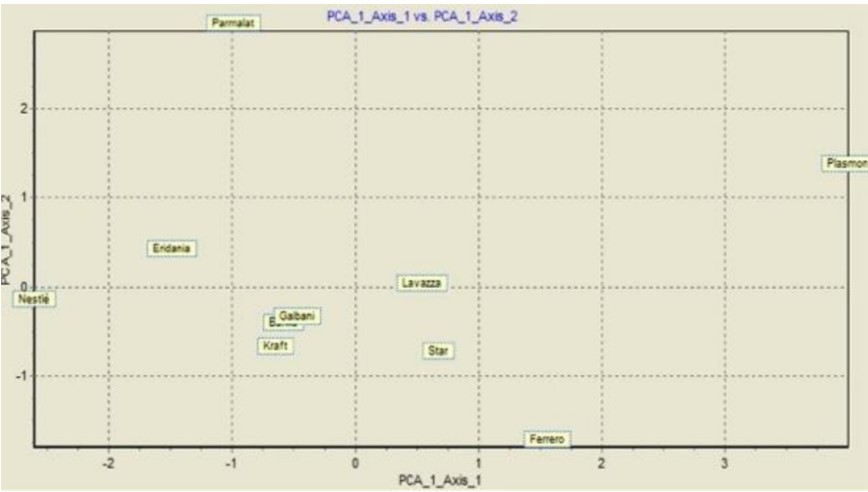
Interpretare: Unele dintre ele sunt pozi?ionate în arii diametral opuse:
?În partea dreapt? jos se situeaz? Ferrero, care este cea mai ”s?n?toas?” companie, având îndatorare negativ? (deci î?i onoreaz? obliga?iile financiare cu capitalul propriu) ?i o profitabilitate convenabil?.
? În cadranul din dreapta sus g?sim compania Plasmon, care de?i are un grad de îndatorare ridicat, are ?i o profitabilitate mare.
? În cadranul din stânga jos se situeaz? companiile care opereaz? în pie?ele saturate unde sunt lideri; în plus, fiind aproape de orginea axelor, sugereaz? c? î?i ?in situa?ia financiar? sub control, având datorii negative de?in rezerve de capital gata s? fie utilizate pentru a îndeplini nevoile pie?ei sau pentru a in?ia ac?iuni pe pia?? în afaceri foarte profitabile.
? În cele din urm?, în cadranul din stânga sus g?sim compania Parmalat: aceasta prezint? cea mai deteriorat? situa?ie. Având atât o îndatorare ridicat?, cât ?i profitabilitate negativ?, aceast? companie trebuie s? î?i regândeasca sistemul de business pentru a evita riscul de insolven??.
Rezumat
Rezumat Click to read  |
 Redare audio
Redare audio

























