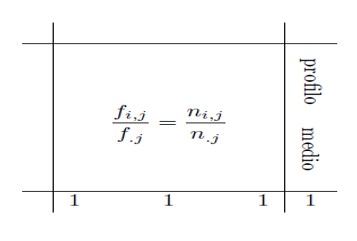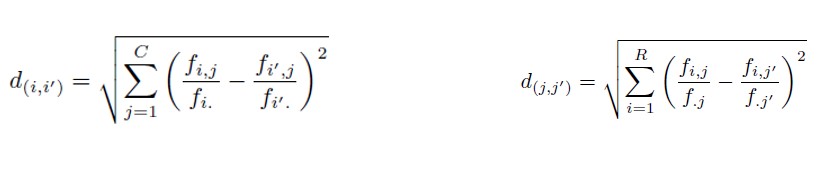|
Analisi delle Corrispondenze
Introduzione
Analisi delle Corrispondenze, AC Click to read 
L'analisi delle corrispondenze è un metodo statistico per l'analisi di dati multidimensionali, è una tecnica multivariata che analizza schemi di associazione tra variabili qualitative.
Le variabili qualitative sono delle variabili che non sono rappresentate da numeri, ma da modalità, esempio: genere, livello di istruzione, stato civile ecc.
Dal momento che nell’AC si utilizzano variabili di tipo qualitativo, oggetto dell'analisi sono le matrici di contingenza. All’interno ci sono ci sono i conteggi congiunti di due diverse grandezze.
Obiettivo dell’ Analisi delle Corrispondenze Click to read 
Obiettivo principale dell’AC è quello di analizzare le relazioni esistenti tra un insieme di variabili qualitative osservate su un collettivo di unità statistiche. Questo avviene attraverso l’identificazione di uno spazio “ottimale”, cioè di una dimensione ridotta che rappresenta la sintesi dell’informazione strutturale contenuta nei dati originari.
In sostanza si andranno a costruire una serie di variabili latenti (o fattori), combinazione delle variabili originali, che esprimono alcuni concetti non direttamente osservabili nella realtà ma frutto della misurazione di un insieme di variabili.
La premessa nell’ Analisi delle Corrispondenze Click to read 
Nell’Analisi delle Corrispondenze le variabili utilizzate non devono essere indipendenti, quindi le modalità di una variabile devono influenzare le modalità dell’altra.
Prima di effettuare un'analisi delle corrispondenze è necessario stabilire il grado di interdipendenza tra i caratteri considerati in quanto, qualora essi risultassero indipendenti, potrebbe non avere senso ricercare le corrispondenze tra di essi.
Si esegue il test del Chi-quadro che valuta eventuali relazioni di interdipendenza tra le variabili qualitative.
Il test parte dell’ipotesi nulla che considera le due variabili indipendenti. L’ipotesi alternativa sarà, dunque, che le due variabili presentano un certo grado di interdipendenza.
Se i risultati del test restituiscono un p-value < 0.05, l’ipotesi nulla può essere rifiutata e di conseguenza le due variabili saranno considerate in un qual modo interdipendenti e si potrà proseguire con l’analisi delle corrispondenze.
Analisi delle Corrispondenze
Tabelle di Contingenza Click to read 
Le tabelle di contingenza contengono le frequenze congiunte delle modalità delle variabili. Date due variabili qualitative X ed Y, la relativa tabella di contingenza conterrà quante volte si presenta una data modalità della variabile X con una data modalità della variabile Y.
 |
X, Y sono le variabili qualitative.
x1 , xx , x3 : sono le modalità della variabile di X
y1 , y2 , y3 : sono le modalità della variabile di Y
ni,j : sono le frequenze congiunte assolute, ossia le frequenze della coppie, esempio n1,1 : X = x1; Y = y1
ni· sono i marginali di riga : 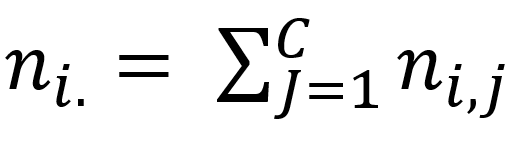
n·j sono i marginali di colonna: 
Questi non sono altro che la somma per la riga fissata (o per la colonna) delle frequenze congiunte sulle modalità di Y (per le colonne sulle modalità di X).
n = è la numerosità campionaria, che si può ottenere sommando i marginali di riga o colonna 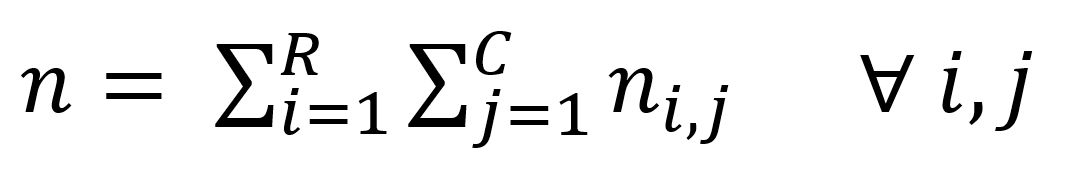
Si può passare dalle frequenze assolute alle frequenze relative dividendo ogni frequenza assoluta per n: 
|
L’analisi delle corrispondenze permette di rappresentare il fenomeno sia nello spazio delle righe, che in quello delle colonne.
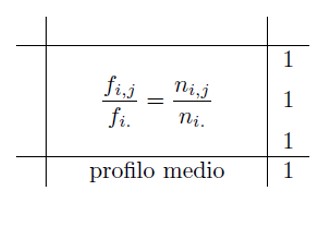
Per fare questo si devono costruire le matrici dei profili riga e colonna: 
-dividendo le frequenze assolute per i corrispondenti marginali di riga (o colonna);
-dividendo le frequenze relative (cioè le frequenze assolute divise per la numerosità totale del campione) per i rispettivi marginali di riga (o colonna).
|
Matrice Profili Riga
|
Matrice Profili Colonna
|
 |
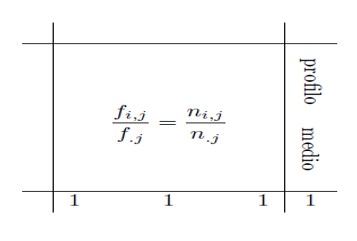 |
Distanze tra i Profili Click to read 
Infine si devono calcolare le distanze tra i profili per vedere se le modalità sono simili o no, lontane o meno, vale a dire vedere se i profili si assomigliano oppure no.
Esistono due tipi di distanze: la distanza euclidea e la distanza del chi-quadro.
-La distanza Euclidea premia le distanze più alte a discapito di quelle più basse e si calcola facendo la differenze tra le frequenze relative e poi si elevano al quadrato.
- La distanza del Chi-quadro, al contrario, premia le distanze più basse in quanto tiene conto della numerosità rispetto alle righe. Si calcola ponderando la differenza delle frequenze relative al quadro per l’inverso del marginale di riga (o colonna).
Un caso Studio
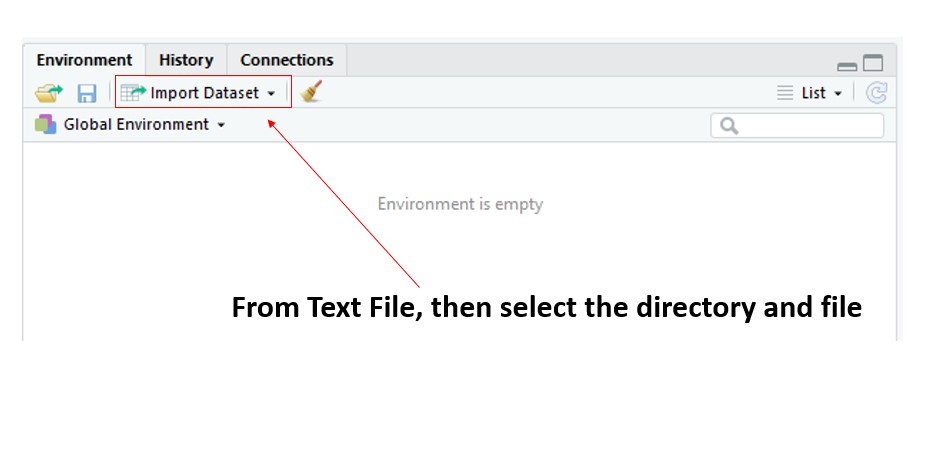
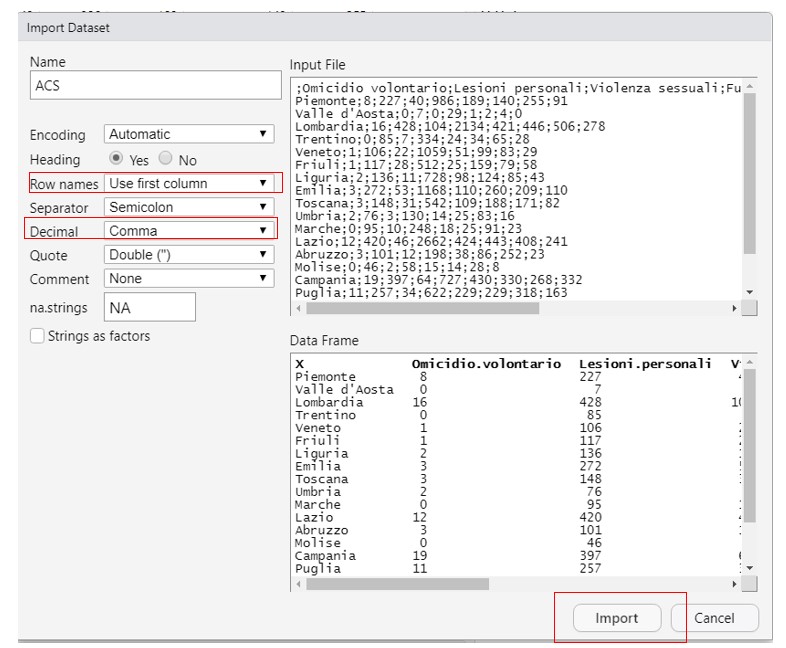
Importare il Dataset Click to read  Test del Chi-quadro Click to read 
|
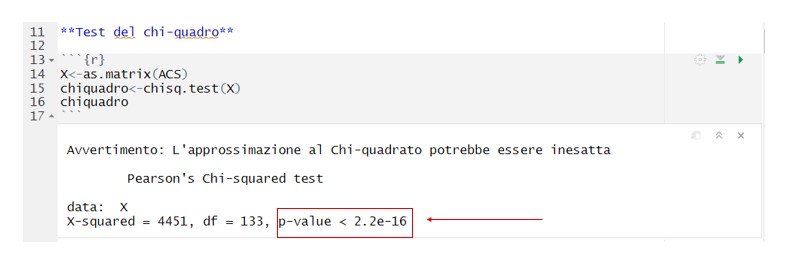
Il test del Chi-quadro è necessario per verificare che le variabili, in questo caso le regioni italiane e i reati commessi in Italia, non siano indipendenti.
L’ipotesi nulla del test sarà: ‘’ Le variabili sono Indipendenti ’’
|
|
| |
|
 |
|
|
Uno dei criteri per rifiutare o non rifiutare l’ipotesi nulla si è quello di osservare il p-value.
Dato un alpha= 5% , il p-value: 2.2e-16.
Dato che il p-value è inferiore del 5%, ossia a 0.05, si rifiuta l'ipotesi nulla, perciò le due variabili si considerano con un certo grado di dipendenza.
|
|
Analisi delle Corrispondenze su R Click to read 
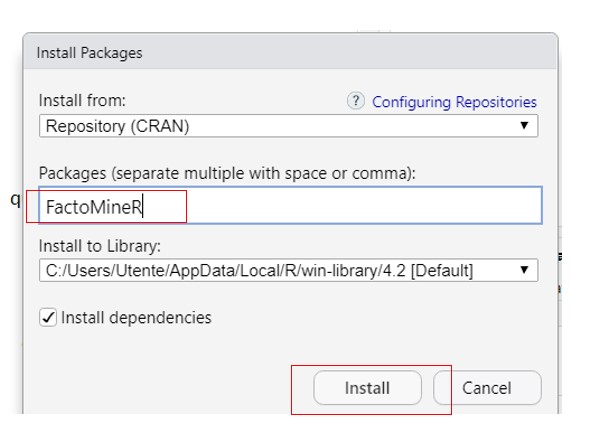
Per l’analisi delle corrispondenze R mette a disposizione un pacchetto denominato FactoMineR.
Come prima cosa è necessario istallare il pacchetto FactoMineR

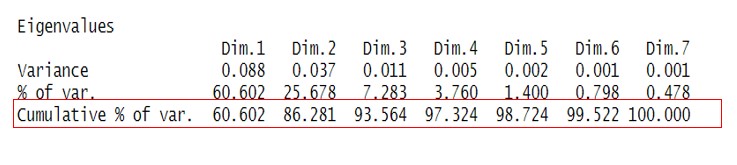 |
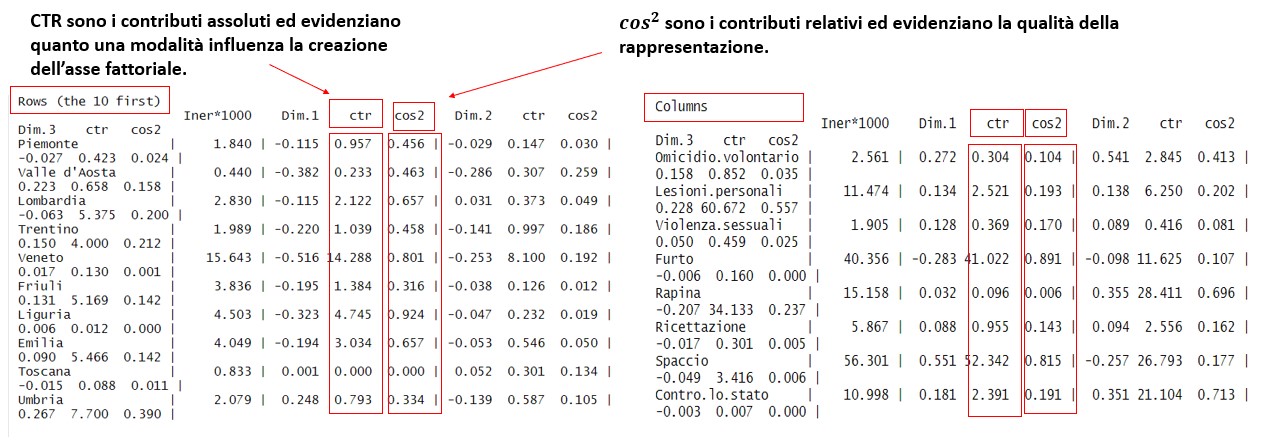
Dato l’obiettivo che si prefissa l’AC, osservando l’inezia spiegata, possiamo vedere a quante dimensioni si riduce il fenomeno.
Vediamo che da sola la prima dimensione spiega circa il 60% della variabilità complessiva dei dati.
|
|
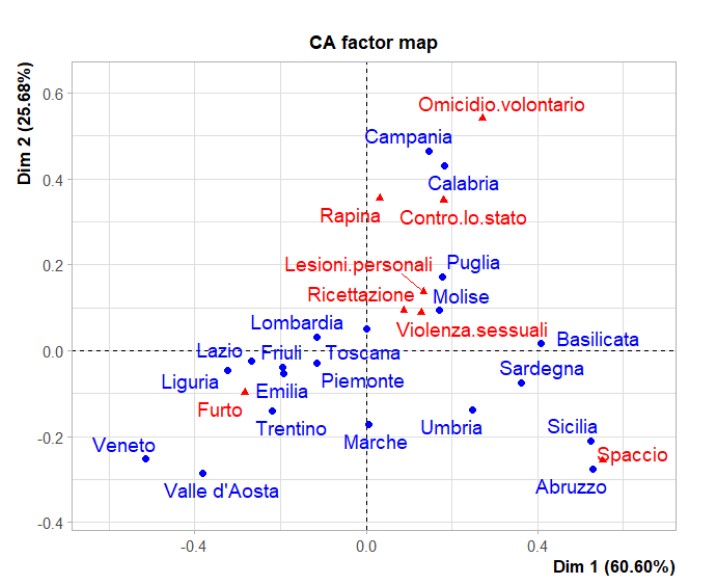
Grafico congiunto bidimensionale individui-variabili rappresenta graficamente come le modalità delle due variabili si dispongono lungo gli assi creati dalle nuove dimensione estratte.
|
 |
Riassumendo
Summing up Click to read  |
 Riprodurre l’audio
Riprodurre l’audio