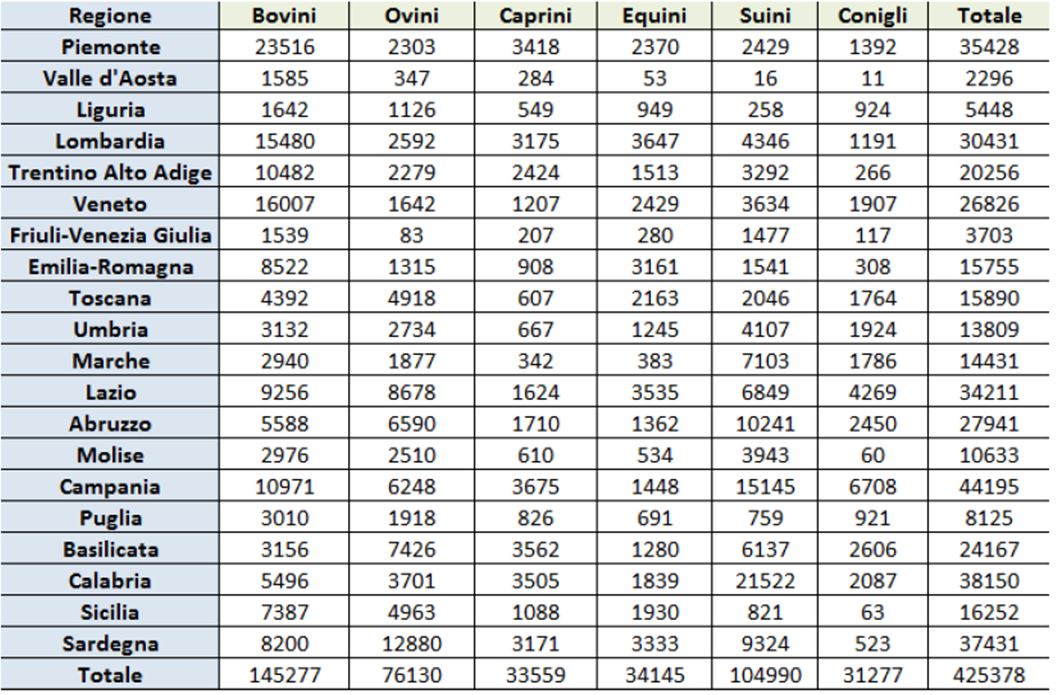
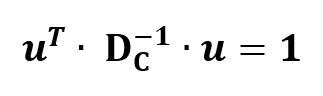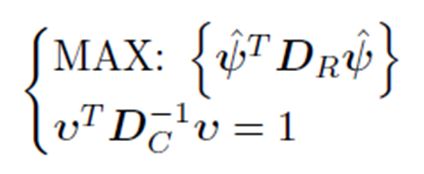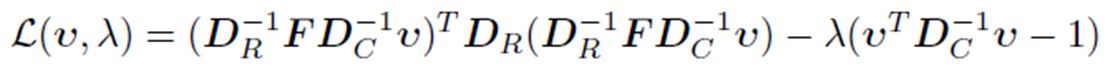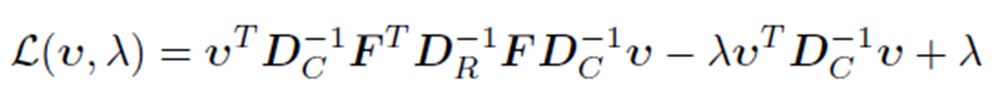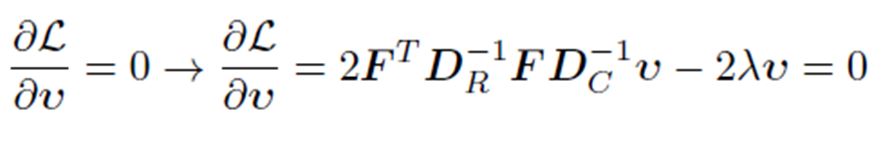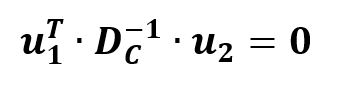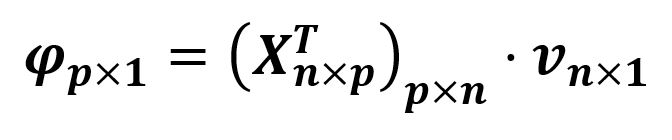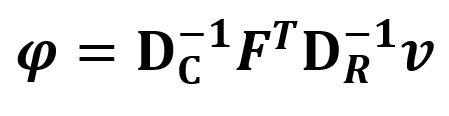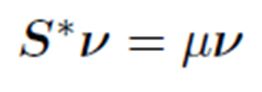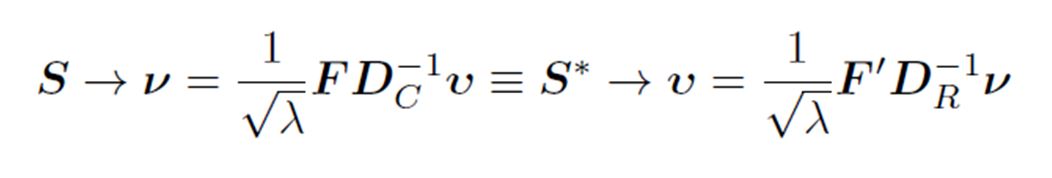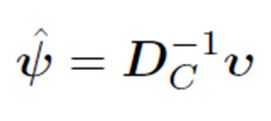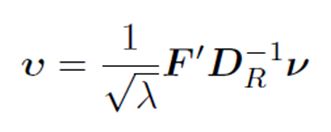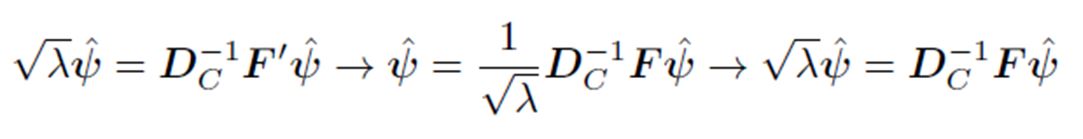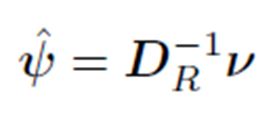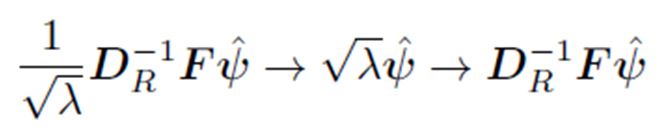Queremos estudiar la posible relación entre las distribuciones del ganado y las diferentes regiones italianas. Los datos se refieren al año 2011, recogidos por los bancos disponibles en la web del Istat.
Hipótesis: las distintas regiones, según las características territoriales y las necesidades de la población, optan por criar unas cabezas de ganado frente a otras.
Conjunto de datos:
Importamos el conjunto de datos:
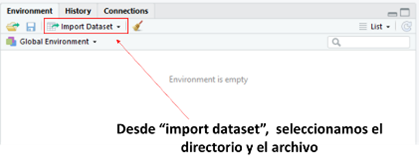
En el campo row names, seleccionamos: “use first column" para tener las etiquetas de individuos y variables en los gráficos.
En el campo decimal seleccionamos "comma".
Con el comando:
X<- as.matrix ( nombre_del_conjunto de datos)
Atribuimos a X, como objeto, el conjunto de datos utilizado en el análisis.
Antes de poder realizar el AC es necesario establecer el grado de interdependencia entre las dos variables consideradas, esto se debe a que en el caso de que sean independientes puede no tener sentido continuar con el AC. Para verificar esto realizamos la prueba de chi-cuadrado.
El comando es:
Nombre del objeto en R<- chisq.test (X)

Se puede observar que el valor de p es inferior al nivel de significación más utilizado, es decir, 0,05. Por lo tanto, podemos rechazar la hipótesis nula de independencia estadística entre las dos variables y podemos continuar con el análisis.
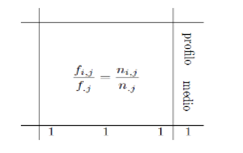
Ahora queremos crear una matriz de frecuencias relativas F.
Calculamos el número de muestra, con el comando:
n<-sum(X)
y luego dividiendo la matriz inicial (por lo tanto todas las frecuencias conjuntas) por el número de muestra obtenemos la matriz F . Dominio:
F<-X/n
El siguiente paso es obtener las tablas de perfiles fila y columna. Para ello, en primer lugar, es necesario calcular las sumas de fila y columna. Respectivamente los comandos son:
umrow<-apply(F,1,sum)
sumcol<-apply(F,2,sum)
Luego calculamos la matriz diagonal de los marginales de fila y su inversa con los comandos:
Dr<-diag(sumrow)
Dr_inv<-solve(Dr)
Ahora podemos calcular perfiles fila. En términos matriciales, premultiplicamos la inversa de la matriz diagonal de la fila marginal a la matriz de frecuencias relativas. El comando a utilizar es:
Pr <- Dr_inv %*%F
Lo mismo para los perfiles de columnas, recordando que en este caso se debe postmultiplicar la inversa de la matriz de columnas por la matriz de frecuencias relativas.
Dc<-diag(sumcol)
Dc_inv<-solve(Dc)
Pc<-F%*%Dc_inv
Ahora podemos calcular las distancias entre los puntos. Como ya se mencionó, hay dos tipos de distancia: euclídea y chi-cuadrado .
Distancia euclídea para perfiles fila:
d_euc_r <- dist ( rbind ( Pr [1,], Pr [2,]))
Distancia euclídea para perfiles columna:
d_euc_c <- dist ( rbind ( Pr [,1], Pr [,2]))
Distancia chi-cuadrado para perfiles fila:
d_r <-pr[1,]-pr[2,]
d<-d_r^2/ sumcol
d_chi_r <-sqrt(sum(d))
Distancia chi-cuadrado para perfiles columna:
dc<-Pr[,1]-Pr[,2]
dc<-dc^2/sumrow
d_chi_c<-sqrt(sum(dc))
La ecuación característica de la matriz de perfiles fila es:
S<-t( Pr )%*%Pc
Como la matriz S no es simétrica, es necesario diagonalizarla para obtener S_tilde :
A<-t(F)%*%Dr_inv%*%F #simmetria
Dc_12<-diag(sumcol^(-1/2))
S_tilde<-Dc_12%*%A%*%Dc_12
Ahora tenemos que maximizar la inercia explicada descomponiendo la matriz en autovalores y vectores propios:
AC<-eigen(S_tilde)
lambda<-as.matrix(AC$values)
lambda<-lambda[-1,]
w<-AC$vectors
u<-Dc^(1/2)%*%w
u<-u[,-1]
La ecuación característica de la matriz de perfiles de columna es:
S_star<-F%*%Dc_inv%*%t(F)%*%Dr_inv
Para pasar de u a v, usamos fórmulas de transición (ya que la cantidad de inercia explicada es igual por filas y columnas).
sq_lambda<-diag((sqrt(lambda))^(-1))
v<-F%*%Dc_inv%*%u%*%sq_lambda
Calculamos factores y coordenadas, primero por filas y luego columnas:
fp_r<-Dc_inv%*%u
fp_c<-Dr_inv%*%v
PHI_coord<-Dc_inv%*%t(F)%*%fp_c
PSI_coord<-Dr_inv%*%F%*%fp_r
Representamos la gráfica con las coordenadas principales:
PRINCOORD<-rbind(PSI_coord,PHI_coord)
rows<-row.names(X);columns<-colnames(X)
plot(PRINCOORD[,1],PRINCOORD[,2],type="n",main="Main Coordinates",xlab="Axis1",ylab="Axis2")+ text(PRINCOORD[1:20,1],PRINCOORD[1:20,2],labels=rows,col="springgreen4")
text(PRINCOORD[21:29,1],PRINCOORD[21:29,2],labels=columns,col="violetred")
abline(h=0,v=0,lty=2,lwd=1.5)
Y así obtenemos:
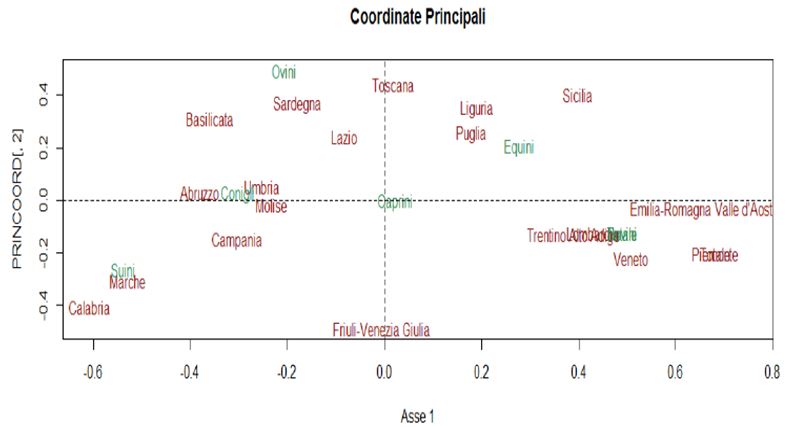
Mirando este gráfico podemos decir, por ejemplo, que en regiones como Abruzzo, Molise o Umbría se crían principalmente conejos.
Seleccionamos los componentes:
inertia<-sum(diag(S))-1
sum(lambda)
in_exp<-lambda/inertia
in_exp_<-cumsum(in_exp)
Y visualizamos los resultados obtenidos:
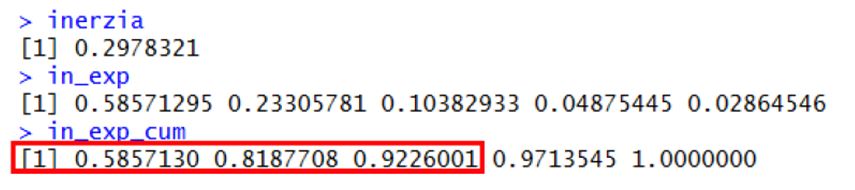
La primera dimensión por sí sola explica el 58,57% de la variabilidad, y las tres primeras juntas explican el 92,26% de la variabilidad global de los datos.
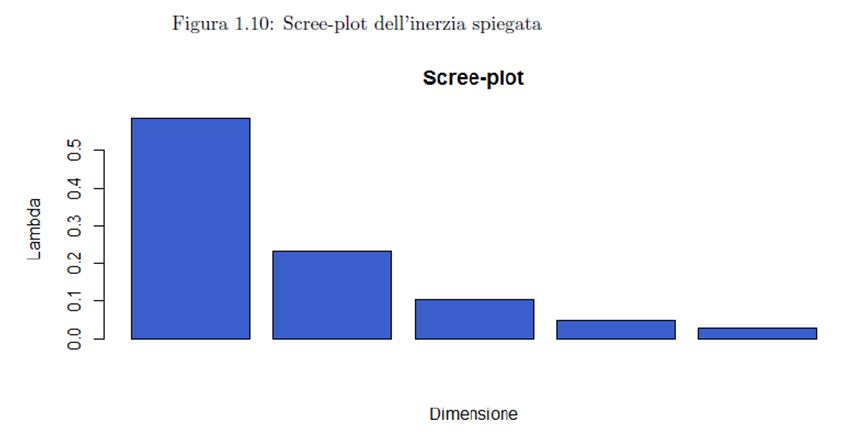
Los resultados obtenidos se pueden visualizar gráficamente con el scree-plot de la inercia explicada:
screeplot<-barplot(in_exp,main="Scree-plot inertia", xlab="Size", ylab="Lambda", col="lightblue")
Para estudiar la calidad de la representación, procedemos como sigue:
- para evaluar cuánto influye o participa una categoría en el eje factorial calculamos las contribuciones absolutas , ca, tanto para filas como para columnas:
ca_r <-Dr%*%fp_c^2
ca_c <-DC%*%fp_r^2
para evaluar la calidad de la representación calculamos las contribuciones relativas, cr. Éstas dan una mejor medida de la representación de los puntos sobre los ejes y vienen dadas por el coseno del ángulo formado por el vector de proyección del punto y el vector relativo i (o j) en el punto i ( o j ) en su espacio G<-matrix(sumcol,20,9,byrow=T)
di<-(Pr-G)^2%*%Dc_inv
d_ig<-apply(di,1,sum)
cos2r<-PSI_coord^2/d_ig
H<-matrix(sumrow,20,9)
dj<-Dr_inv%*%(Pc-H)^2
d_jh<-apply(dj,2,sum)
COS2C<-PHI_coord^2/d_jh
R posibilita emplear un paquete llamado FactoMineR para el análisis de correspondencias, que agrega información sobre puntos y variables y permite crear un gráfico bidimensional conjunto. Para poder usar este paquete de R primero debes descargarlo:
Después de instalarlo, debe llamarlo con el comando:
library(FactoMineR)
Pasemos a la creación del gráfico bidimensional para puntos y variables:
CA(X, ncp = 5, row.sup = NULL, col.sup = NULL, quanti.sup=NULL, quali.sup = NULL, graph = TRUE, axes = c(1,2), row.w = NULL)
Gráficamente tendremos:
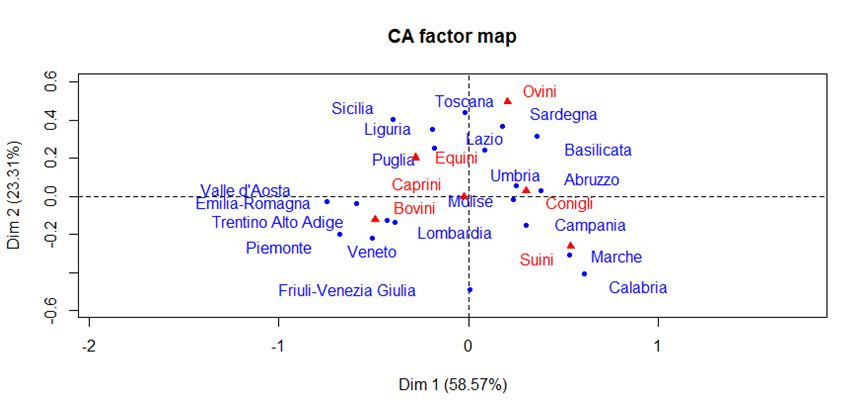
Interpretación de resultados:
Podemos decir que se confirma la hipótesis inicial. En particular, las regiones más dedicadas a la ganadería ovina parecen ser Toscana, Cerdeña y Basilicata, y esto puede explicarse por el hecho de que estas regiones son áreas de montaña y trashumancia. Los caballos se crían principalmente en Puglia, Liguria y Sicilia porque estos animales siempre se han utilizado para el trabajo en el campo. El ganado está presente en Trentino Alto-Adige, Veneto, Piamonte, Lombardía y Emilia-Romaña. De hecho, estas regiones tienen una tradición de crianza más desarrollada para uso alimentario. Los conejos aparecen principalmente en Umbria, Abruzzo y Molise. En cambio, parece que los cerdos se crían más en Marche, Campania y Molise. Estas regiones también tienen una tradición de cría más desarrollada para uso alimentario.Las cabras, en cambio, se colocan en medio de los ejes, probablemente porque no hay regiones que prefieran su cría.
 Reproducir el audio
Reproducir el audio 






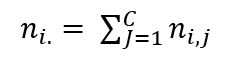

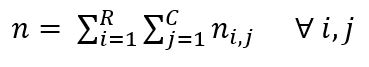



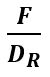 . Las dimensiones de F son R· C, mientras que DR tiene dimensión R· R, como no se puede hacer la división entre matrices, se calcula la inversa DR y se multiplica por F , resolviendo así el problema de dimensionalidad: DR-1·F.
. Las dimensiones de F son R· C, mientras que DR tiene dimensión R· R, como no se puede hacer la división entre matrices, se calcula la inversa DR y se multiplica por F , resolviendo así el problema de dimensionalidad: DR-1·F.
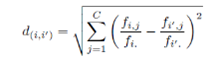
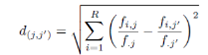
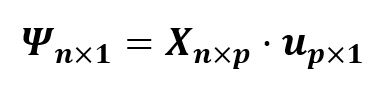
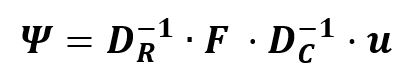
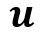 pueden ser infinitos, se agrega la restricción de la norma unitaria.
pueden ser infinitos, se agrega la restricción de la norma unitaria.