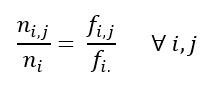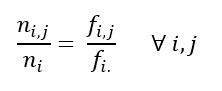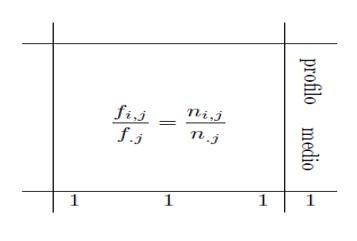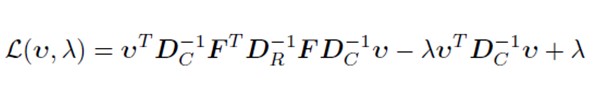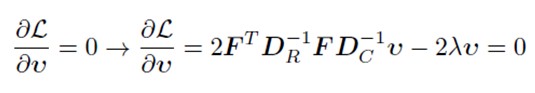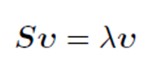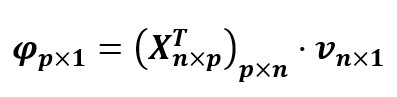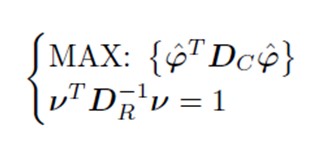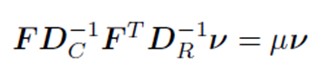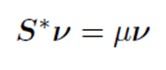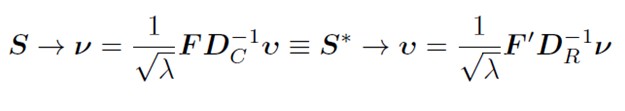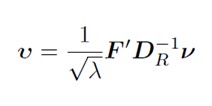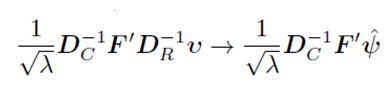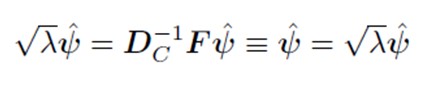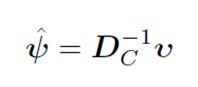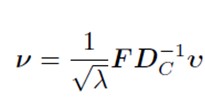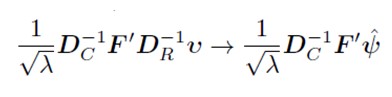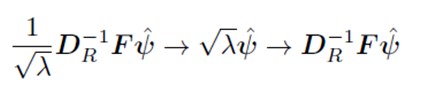Analiza coresponden?ei, AC, este o tehnic? de analiz? multidimensional? care poate traduce aproape orice tip de tabel format din date numerice într-o form? grafic?. Obiectul AC sunt matricele de contingenta, ale c?ror elemente indic? de câte ori caracteristicile a dou? cantit??i diferite au fost detectate împreun?. Scopul principal al AC este de a analiza rela?iile dintre dou? variabile calitative observate într-un colectiv de unit??i statistice. Acest lucru se realizeaz? prin identificarea unui spa?iu "optimal", adic? a unei dimensiuni reduse care reprezint? sinteza informa?iilor structurale con?inute în datele ini?iale. Scopul analizei este de a eviden?ia împletirea leg?turilor sau coresponden?elor care exist? între datele examinate.

Pentru a efectua o analiz? a coresponden?ei, este important s? analiz?m variabilele care urmeaz? s? fie utilizate ?i s? în?elegem clar unele dintre caracteristicile lor. În mod specific, variabilele trebuie s? îndeplineasc? urm?toarele cerin?e:

•  Variabilele trebuie s? fie calitative:

Variabilele calitative nu sunt reprezentate de numere, ci de modalit??i sau categorii. De exemplu, genul, nivelul de educa?ie, starea civil? etc. Aceste modalit??i trebuie s? fie exhaustive ?i mutual exclusive. Mutual exclusive înseamn? c? modalit??ile variabilelor nu trebuie s? con?in? acela?i tip de informa?ie. De exemplu, pentru variabila "culoarea p?rului", nu se pot introduce modalit??ile "p?r închis" ?i "p?r brun", deoarece "p?r închis" înseamn? ?i "p?r brun" ?i viceversa. ”Exhausitv” înseamn? c? modalit??ile unei variabile trebuie s? acopere toate posibilit??ile. De exemplu, pentru variabila "nivelul de educa?ie", se introduc modalit??ile "diplom?", "licen??", "masterat". Aceste trei modalit??i nu acoper? toate posibilit??ile de nivel de educa?ie.

• Variabilele trebuie s? fie interdependente:

Înainte de a efectua analiza coresponden?elor, este necesar s? verific?m gradul de interdependen?? între cele dou? variabile luate în considerare, deoarece, în cazul în care acestea ar fi independente, analiza coresponden?elor ar putea s? nu aib? sens.
Pentru a face acest lucru, se realizeaz? testul chi-p?trat:
H_0: cele dou? variabile sunt independente
H_1: cele dou? variabile nu sunt independente
Pentru a interpreta rezultatele testului, observ?m valoarea p:
valoarea p < 0,05: ipoteza nul? este respins? ?i, în consecin??, variabilele sunt considerate a fi interdependente într-o anumit? m?sur?.
 

Dup? ce a?i verificat cerin?ele pentru AC, pute?i trece la analiza efectiv?.

În analiza coresponden?elor lucr?m cu tabele de contingenta, care con?in frecven?ele conjuncte ale modalit??ilor celor dou? variabile calitative X ?i Y. Aceste matrici sunt întotdeauna alc?tuite din numere întregi niciodat? negative care reprezint? num?rul de apari?ii, adic? înregistr?ri simple ale ceea ce s-a întâmplat. În plus, ambele variabile categoriale au un rol simetric în care toate elementele au aceea?i natur?.

Matricea profilurilor de rând este ob?inut? prin împ?r?irea frecven?elor absolute (sau frecven?elor relative) la frecven?ele marginale de rând corespunz?toare. Prin urmare:

Tabelul de contingen?? devine:

Pe marginea de rând avem întotdeauna 1 ?i aceasta reprezint? suma profilurilor de rând.

Pe marginea coloanei se g?sesc profilurile medii, care sunt ob?inute prin adunarea frecven?elor relative pe coloan?; sau prin calcularea mediei elementelor matricei profilului de rând, pe coloan?. Aceasta este o medie ponderat?, în care ponderile sunt reprezentate de frecven?ele marginale de rând f_i .  
Lucrând cu frecven?e, se pierde o dimensiune, astfel încât spa?iul de rând este reprezentat de un spa?iu cu C-1 dimensiuni; Se poate construi o matrice diagonal? a frecven?elor marginale de rând D_R, care are profilurile de rând pe diagonala principal?. Matricea diagonal? a frecven?elor marginale de rând este o matrice R· R, care are dimensiuni egale cu num?rul de rânduri ?i pe diagonala principal? con?ine frecven?ele marginale de rând a tabelului de frecven?e relative. O matrice diagonal? este o matrice ale c?rei elemente generice de pe diagonala principal? sunt marginalii de rând, iar deasupra sau dedesubtul acesteia exist? doar zero-uri. Este întotdeauna o matrice simetric? ?i p?trat?. Cu matricea diagonal? a marginalilor de rând se poate construi matricea profilurilor de rând: aceasta se ob?ine prin împ?r?irea frecven?elor relative la marginalii de rând F/D_R.  Dimensiunile matricei F sunt R · C, în timp ce matricea D_R are dimensiunea R· R. Deoarece nu se poate face împ?r?irea direct? între matrice, se calculeaz? inversa matricei D_R ?i se înmul?e?te cu matricea F, rezolvând astfel problema dimensionalit??ii. : D_R ^-1. F .
Acela?i lucru se aplic? ?i pentru coloane, cu unele mici diferen?e. Matricea profilurilor de coloan? este construit? prin împ?r?irea frecven?elor absolute la marginalii relative de coloan?:

Tabelul de contingen?? devine:

În acest caz, pe marginea coloanei ve?i avea întotdeauna 1, iar pe marginea de rând ve?i avea profilul mediu al coloanei. În acest caz, ponderile sunt reprezentate de marginalii de coloan? f.j. Evident, chiar ?i în spa?iul de coloan? se lucreaz? cu mai pu?in de o dimensiune, deci spa?iul de coloan? este R-1. 
Se poate construi o matrice diagonal? a marginalilor de coloan? D_c, care are profilurile de coloan? pe diagonala principal?. Matricea diagonal? a marginalilor de coloan? este o matrice C·C, care are dimensiuni egale cu num?rul de coloane ?i pe diagonala principal? con?ine marginalii de coloan? ai tabelului de frecven?e relative. O matrice diagonal? este o matrice ale c?rei elemente generice de pe diagonala principal? sunt marginalii de coloan?, iar deasupra sau dedesubtul acesteia exist? doar zero-uri. Este întotdeauna o matrice simetric? ?i p?trat?. 
Cu matricea diagonal? a marginalilor de coloan?: aceasta se ob?ine prin împ?r?irea frecven?elor relative la marginalii de coloan? F/D_R. Dimensiunile matricei F sunt R · C, în timp ce matricea D_c  are dimensiunea C · C. Deoarece împ?r?irea între matrici nu poate fi efectuat? direct, se calculeaz? inversa matricei D_C    ?i se înmul?e?te cu F prin post-înmul?ire, rezolvând astfel problema dimensionalit??ii:  F . D_c ^-1 

În analiza coresponden?elor este necesar s? în?elegem ce distan?? exist? între valorile respective, în scopul de a în?elege dac? modalit??ile sunt apropiate sau îndep?rtate una de cealalt? ?i, prin urmare, dac? se aseam?n? sau nu. Acest lucru poate fi realizat prin observarea frecven?elor: cu cât sunt mai mici, cu atât sunt mai apropiate, ?i viceversa. Exist? diferite metode de calcul al distan?ei, cum ar fi distan?a euclidian? ?i distan?a chi-p?trat.

Distan?a euclidian? este cea mai simpl? ?i acord? mai mult? importan?? diferen?elor mari în defavoarea celor mici. Se calculeaz? prin diferen?a dintre frecven?ele relative ?i ridicarea lor la p?trat.

Pentru profilurile de rând:                        Pentru profilurile de coloan?:

Distan?a chi-p?trat recompenseaz? distan?ele mai mici deoarece frecven?ele cu valori mici sunt reponderate în raport cu rândurile, introducând în formul? inversul frecven?elor marginale de coloan? (respectiv inversul frecven?elor marginale de rând). Dezavantajul distan?ei chi-p?trat este c? valoarea reciproc? a frecven?elor marginale de coloan? (sau de rând) poate tinde c?tre zero ?i, prin urmare, o singur? valoare poate contribui excesiv la calculul distan?ei.

În spa?iul rândurilor cele dou? componente sunt: 

• Profile de rând:  DR-1?F
• Metrica: DC-1

S? începem cu urm?toarea formul?:

Dup? înlocuirile adecvate rezult?:

Obiectivul analizei coresponden?elor const? în g?sirea setului de axe unitare care permite maximizarea distan?elor dintre proiec?iile profilurilor de rând. Trebuie, a?adar, s? c?ut?m acei vectori care maximizeaz? proiec?iile. Deoarece vectorii u pot fi infini?i, se adaug? restric?ia normei unitare.

Problema de maximizare: Se maximeaz? iner?ia explicat? (varia?ia explicat?), care corespunde variabilit??ii pentru variabilele cantitative.

Pentru a rezolva problema de maximizare cu restric?ii, utiliza?i metoda multiplicatorilor Lagrange:

= multiplicatorul Lagrange, care este un scalar;

u=  vectorul ponderilor, pe care dorim s? îl determin?m

Prin efectuarea înlocuirilor necesare, vom avea:

Efectu?m opera?iile de transpunere, înlocuim matricea identitate I cu o   ?i   o înlocuim cu .  WPutem apoi elimina transpusa din matricile diagonale ?i  , deoarece transpusa unei matrice diagonale nu se modific?.

Rezult?:

Calcul?m derivatele par?iale, derivând Lagrange-anul în raport cu u ?i le egal?m cu 0:

Se înmul?e?te ecua?ia cu  :

Dac? înlocuim transpunerea profilelor de rând ?i matricea profilelor de coloan? cu S, putem scrie ecua?ia caracteristic? sub forma:

Maximizarea iner?iei explicate a profilelor de rânduri este echivalent? cu descompunerea acestei matrice în valori proprii ?i vectori proprii ai acesteia. Prima valoare proprie este asociat? cu primul vector propriu care explic? iner?ia maxim?. Vectorii proprii care se extrag ulterior vor fi extra?i ortogonal, aplicând constrângerea de ortogonalitate:

Utiliz?m constrângerea de ortogonalitate pentru a putea alege cea de-a doua component? care va explica iner?ia care nu este explicat? de prima component?. Evident, prima component? extras? explic? iner?ia maxim?, adic? alungirea maxim? a norului de puncte. 

În spa?iul coloanelor sunt dou? componente:

• Profilul de coloana: 
• Metrica:

Începem cu formula:

Dup? înlocuire, se ob?ine:

Problema de maximizare care trebuie rezolvat? cu multiplicatori Lagrange este:

Procedând ca în spa?iul rândurilor, în final vom ob?ine:

Înlocuind matricea profilelor de coloan? ?i metrica transpus? a profilelor de rând cu  se ob?ine ecua?ia caracteristic?:

Maximizarea geometric? a iner?iei explicate, ?i anume, realizarea unei cantit??i cât mai mici de informa?ii pierdute ?i a unei cantit??i cât mai mari de informa?ii observate, va fi urm?toarea: distan?a s? fie cât mai mic? ?i distan?a  cât mai mare.

Prin urmare, trebuie s? g?sim dreapta f (în ro?u) care interpoleaz? punctele din spa?iul vectorial, astfel încât distan?a dintre toate punctele din spa?iu ?i punctele proiectate ortogonal pe dreapta f s? fie cea mai mic? posibil?.
Valorile proprii în spa?iul liniilor corespund vectorilor proprii în spa?iul coloanelor, astfel încât valorile proprii ale lui S corespund celor ale lui S* . Vectorii proprii sunt egali între ei, cu excep?ia unei constante. Astfel, atunci când trebuie s? maximiz?m, nu trebuie s? descompunem în valori proprii ?i vectori proprii S ?i S* , ci doar s? o facem cu unul singur.  Cantitatea de iner?ie explicat? este egal? indiferent dac? calcul?m  S sau S* , rela?ia dintre cele dou? spa?ii este reprezentat? de formulele de tranzi?ie:

Spa?iul rândurilor: 

Cu:

Dup? efectuarea substitu?iilor corespunz?toare, se ob?ine:

Rezult?:

Pentru spa?iul rândurilor:

Spa?iul coloanelor:

Unde:

Dup? efectuarea substitu?iilor corespunz?toare, se ob?ine:

Rezult?:

 Pentru spa?iul coloanelor:

Verificarea unei posibile rela?ii între distribu?ia animalelor ?i diferitele regiuni italiene. Datele se refer? la anul 2011, colectate de c?tre b?ncile disponibile pe site-ul Istat.
Ipotez?: diferitele regiuni, în func?ie de caracteristicile teritoriale ?i de nevoile popula?iei, aleg s? creasc? anumite capete de bovine mai degrab? decât altele.
Setul de date:

Import?m setul de date:

În câmpul "Row names" (Nume rânduri), selecta?i formularea: "use first column" (utiliza?i prima coloan?) pentru a avea etichetele atât ale indivizilor, cât ?i ale variabilelor pe grafice. În câmpul zecimale, select?m " comma " (virgul?).

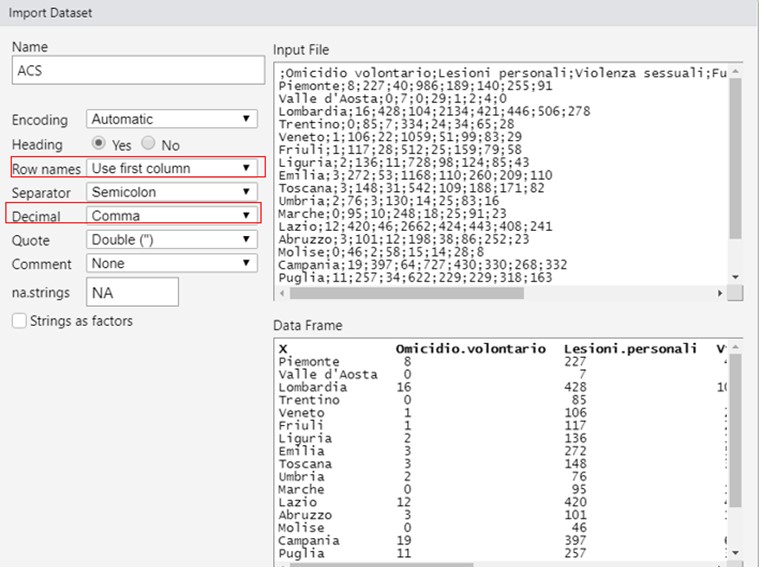
With the command:

X<-as.matrix(nome_del_dataset)

Atribuim lui X, ca obiect, setul de date utilizat în analiz?.

Înainte de a putea efectua AC este necesar s? se stabileasc? gradul de interdependen?? dintre cele dou? personaje luate în considerare, aceasta deoarece în cazul în care acestea sunt independente s-ar putea s? nu aib? sens s? se continue AC. Pentru a verifica acest lucru, efectu?m testul chi-p?trat.

chiquadro<-chisq.test(X)

Comanda este urm?toarea:

Se poate observa c? valoarea p este mai mic? decât nivelul de semnifica?ie cel mai frecvent utilizat, ?i anume 0,05. Prin urmare, putem respinge ipoteza nul? de independen?? statistic? între cele dou? variabile ?i putem continua analiza.

Acum dorim s? cre?m o matrice de frecven?e relative F.

Calcul?m num?rul de e?antioane, cu comanda:

n<-sum(X)

?i apoi împ?r?ind matricea de pornire (deci toate frecven?ele comune) la num?rul de e?antioane se ob?ine matricea F. Comand?:

F<-X/n

Urm?torul pas este ob?inerea tabelelor de profiluri de rânduri ?i coloane. Pentru a face acest lucru, în primul rând, este necesar s? se calculeze marginalele rândului ?i ale coloanei. Respectiv, comenzile sunt:

sumrow<-apply(F,1,sum)

sumcol<-apply(F,2,sum)

Apoi calcul?m matricea diagonal? a frecven?elor marginale de rând ?i inversa acesteia cu ajutorul comenzilor:

Dr<-diag(sumrow)

Dr_inv<-solve(Dr)

Acum putem calcula profilurile rândurilor. În termeni matriciali, înmul?im în prealabil inversa matricei diagonale a rândului marginal cu matricea frecven?elor relative. Comanda care trebuie folosit? este:

Pr<-Dr_inv%*%F

Acela?i lucru pentru profilurile coloanelor, ?inând cont de faptul c?, în acest caz, inversa matricei coloanelor trebuie s? fie post-multiplicat? la matricea frecven?elor relative.

Dc<-diag(sumcol)

Dc_inv<-solve(Dc)

Pc<-F%*%Dc_inv

Acum putem calcula distan?ele dintre puncte. Dup? cum am men?ionat deja, exist? dou? tipuri de distan?e: Euclidian? ?i Chi-p?trat.

Profilele rândurilor de distan?e euclidiene sunt:

d_euc_r<-dist(rbind(Pr[1,],Pr[2,]))

Profilele coloanelor de distan?e euclidiene sunt:

d_euc_c<-dist(rbind(Pr[,1],Pr[,2]))

Profilele rândurilor de distan?e chi-p?trat sunt:

d_r<-pr[1,]-pr[2,]

d<-d_r^2/sumcol

d_chi_r<-sqrt(sum(d))

Profilele coloanelor de distan?e chi-p?trat sunt:

dc<-Pr[,1]-Pr[,2]

dc<-dc^2/sumrow

d_chi_c<-sqrt(sum(dc))

Ecua?ia caracteristic? a matricei profilului de rânduri:

S<-t(Pr)%*%Pc

Deoarece matricea S nu este simetric?, este necesar s? o diagonaliz?m pentru a ob?ine S_tilde:

A<-t(F)%*%Dr_inv%*%F #simmetria

Dc_12<-diag(sumcol^(-1/2))

S_tilde<-Dc_12%*%A%*%Dc_12

Acum trebuie s? maximiz?m iner?ia explicat? prin descompunerea matricei în valori proprii ?i vectori proprii:

AC<-eigen(S_tilde)

lambda<-as.matrix(AC$values)

lambda<-lambda[-1,]

w<-AC$vectors

u<-Dc^(1/2)%*%w

u<-u[,-1]

Ecua?ia caracteristic? a matricei profilului de coloane:

S_star<-F%*%Dc_inv%*%t(F)%*%Dr_inv

Pentru a ne deplasa de la u la v, folosim formule de tranzi?ie (deoarece cantitatea de iner?ie explicat? este egal? atât în spa?iul rândurilor, cât ?i în cel al coloanelor).

sq_lambda<-diag((sqrt(lambda))^(-1))

v<-F%*%Dc_inv%*%u%*%sq_lambda

Calcul?m factorii ?i coordonatele, mai întâi spa?iul rândurilor ?i apoi al coloanelor: 

fp_r<-Dc_inv%*%u

fp_c<-Dr_inv%*%v

PHI_coord<-Dc_inv%*%t(F)%*%fp_c

PSI_coord<-Dr_inv%*%F%*%fp_r

Se afi?eaz? graficul coordonatelor principale:

PRINCOORD<-rbind(PSI_coord,PHI_coord)

rows<-row.names(X);columns<-colnames(X)

plot(PRINCOORD[,1],PRINCOORD[,2],type="n",
main="Main Coordinates",xlab="Axis1",ylab="Axis2")+ text(PRINCOORD[1:20,1],PRINCOORD[1:20,2],labels=rows,col="springgreen4")

text(PRINCOORD[21:29,1],PRINCOORD[21:29,2],labels=columns,col="violetred")

abline(h=0,v=0,lty=2,lwd=1.5)

Rezult?:

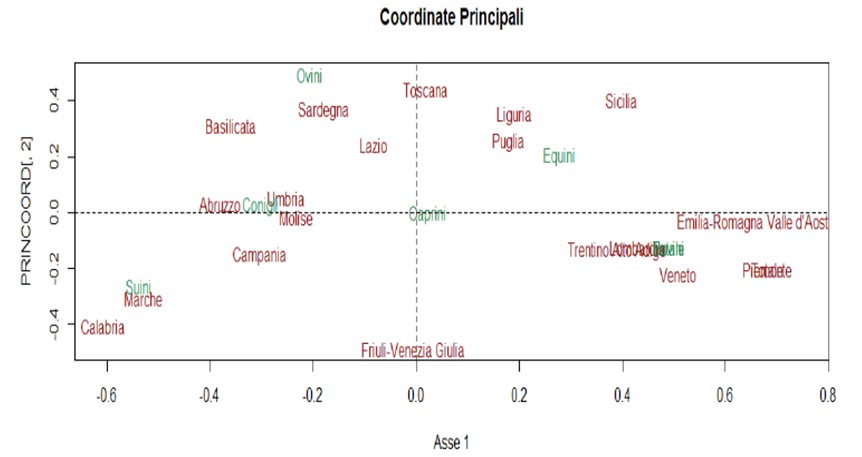
Dac? ne uit?m la acest grafic, putem spune, de exemplu, c? în regiuni precum Abruzzo, Molise, Umbria se cresc în principal iepuri. 
Alegem componentele

inertia<-sum(diag(S))-1

sum(lambda)

in_exp<-lambda/inertia

in_exp_<-cumsum(in_exp)

Vizualiz?m rezultatele ob?inute:

Prima dimensiune explic? singur? 58,57% din variabilitate, iar primele trei împreun? explic? 92,26% din variabilitatea global? a datelor.
Rezultatele ob?inute pot fi afi?ate grafic cu ajutorul graficului scree-plot a iner?iei explicate:

screeplot<-barplot(in_exp,main="Scree-plot inertia", xlab="Size", ylab="Lambda", col="lightblue")

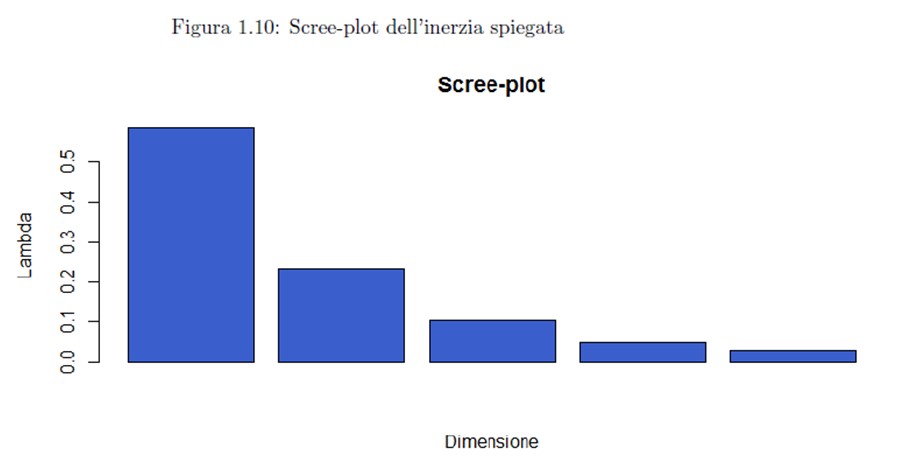
Pentru calitatea reprezent?rii:

• pentru a evalua cât de mult influen?eaz? sau particip? un mod la axa factorial?, se calculeaz? contribu?iile absolute, CA, atât pentru rânduri, cât ?i pentru coloane:

ca_r<-Dr%*%fp_c^2

ca_c<-DC%*%fp_r^2

• Pentru a evalua calitatea reprezent?rii, calcul?m contribu?iile relative, CR. Acestea ofer? o m?sur? mai bun? a reprezent?rii punctelor pe axe ?i este dat? de cosinusul unghiului format de vectorul de proiec?ie al punctului ?i vectorul relativ i (sau j) în punctul i (sau j) din spa?iul s?u original:

G<-matrix(sumcol,20,9,byrow=T)

di<-(Pr-G)^2%*%Dc_inv

d_ig<-apply(di,1,sum)

cos2r<-PSI_coord^2/d_ig

H<-matrix(sumrow,20,9)

dj<-Dr_inv%*%(Pc-H)^2

d_jh<-apply(dj,2,sum)

COS2C<-PHI_coord^2/d_jh

R ofer? un pachet numit FactoMineR pentru analiza coresponden?elor, care adaug? informa?ii despre indivizi ?i variabile ?i v? permite s? crea?i un grafic bidimensional comun al indivizilor ?i variabilelor. 
Pe R pentru a putea utiliza acest pachet trebuie mai întâi s? îl desc?rca?i:

Dup? ce l-a?i instalat, trebuie s? îl apela?i cu comanda
library(FactoMineR)

S? trecem la crearea graficului bidimensional Persoane ?i variabile:

CA(X, ncp = 5, row.sup = NULL, col.sup = NULL, quanti.sup=NULL, quali.sup = NULL, graph = TRUE, axes = c(1,2), row.w = NULL)

Grafic, ob?inem:

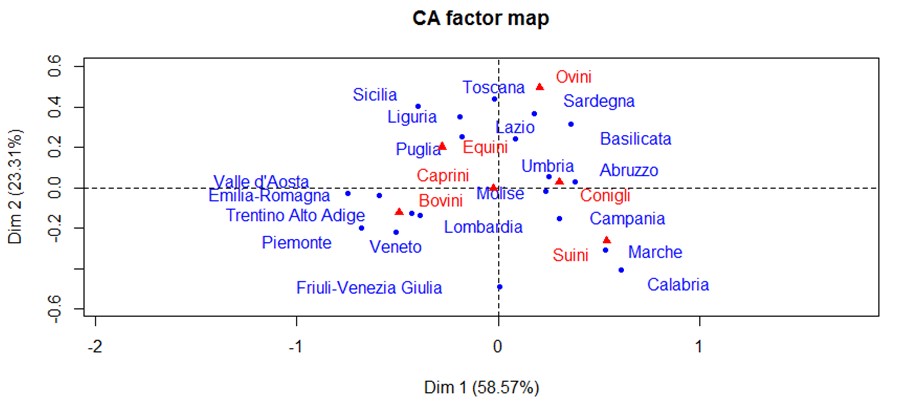
Interpretarea rezultatelor:
Putem spune c? ipoteza ini?ial? este confirmat?.  În special, regiunile cele mai dedicate cre?terii ovinelor par a fi Toscana, Sardinia ?i Basilicata, iar acest lucru poate fi explicat prin faptul c? aceste regiuni sunt zone de munte ?i de transhuman??. Caii sunt crescu?i mai ales în Puglia, Liguria ?i Sicilia, deoarece aceste animale au fost întotdeauna folosite pentru munc? în mediul rural. Bovinele sunt prezente în Trentino Alto-Adige, Veneto, Piemont, Lombardia ?i Emilia-Romagna; de fapt, aceste regiuni au o tradi?ie de cre?tere mai dezvoltat? pentru uz alimentar. Iepurii apar mai ales în Umbria, Abruzzo ?i Molise. În schimb, porcii par s? fie crescu?i mai mult în Marche, Campania ?i Molise; Aceste regiuni au, de asemenea, o tradi?ie de cre?tere mai dezvoltat? pentru uz alimentar.
Caprele, pe de alt? parte, sunt plasate la mijlocul axei, probabil pentru c? nu exist? regiuni care s? prefere cre?terea lor.