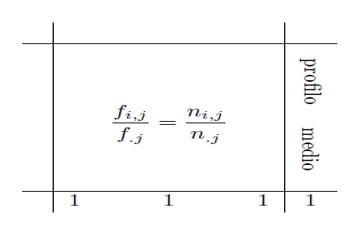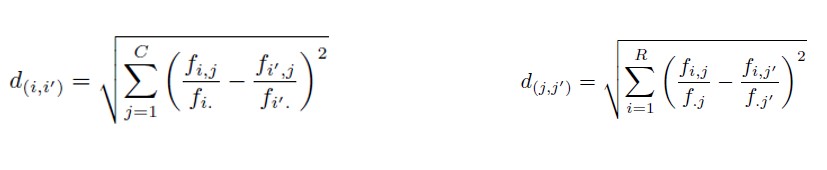DataScience Training
Keywords
Keywords (meta tags) AC, qualitative variables, explained inertia, eigenvalues
Objectives/goals:The aim of this module is to introduce and explain the Principal Component Analysis technique.
At the end of this module you will be able to:
- Know the logic of AC
- Know the requirements
- Conduct an AC
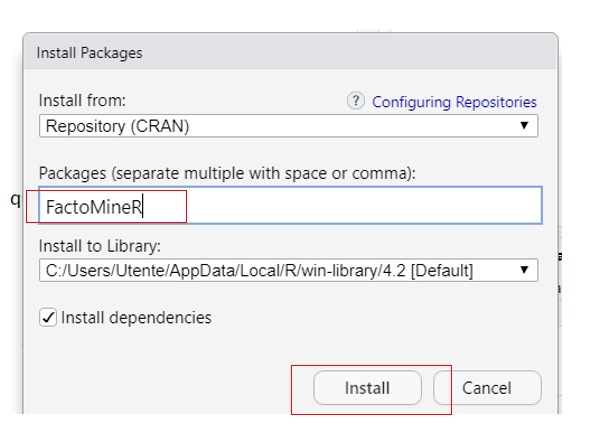
- Conduct an AC in R with the FactoMineR package
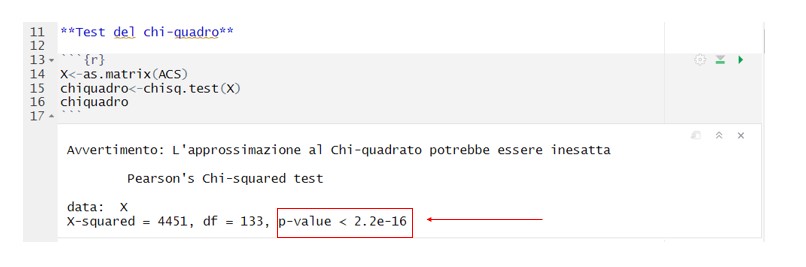
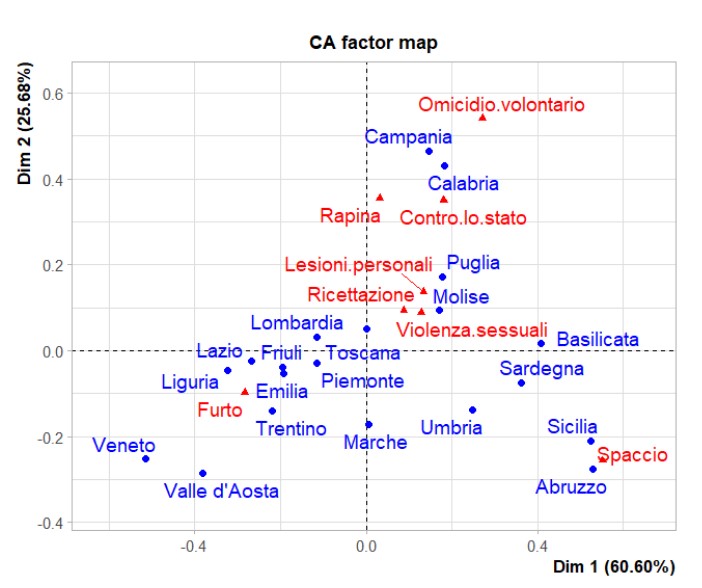
In this training module you will be presented the multidimensional analysis technique called Correspondence Analysis, AC.
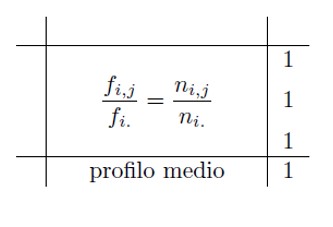
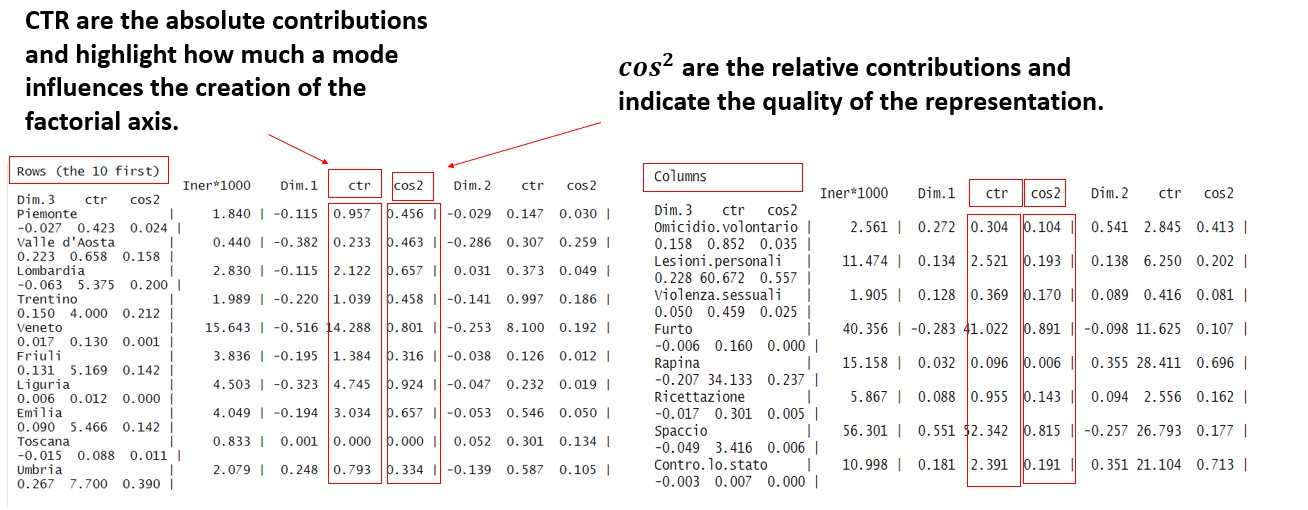
Correspondence Analysis is a form of multidimensional scaling, which essentially builds a kind of spatial model that shows the associations between a set of categorical variables. If the set includes only two variables, the method is usually called Simple Correspondence Analysis (SCA). If the analysis involves more than two variables, then it is usually called Multiple Correspondence Analysis (MCA). In this module we will deal with the analysis of simple correspondences, the objective of this analysis is to reduce the dimensionality of the phenomenon under investigation while preserving the information contained by it. The technique is applicable to phenomena measured with qualitative variables.
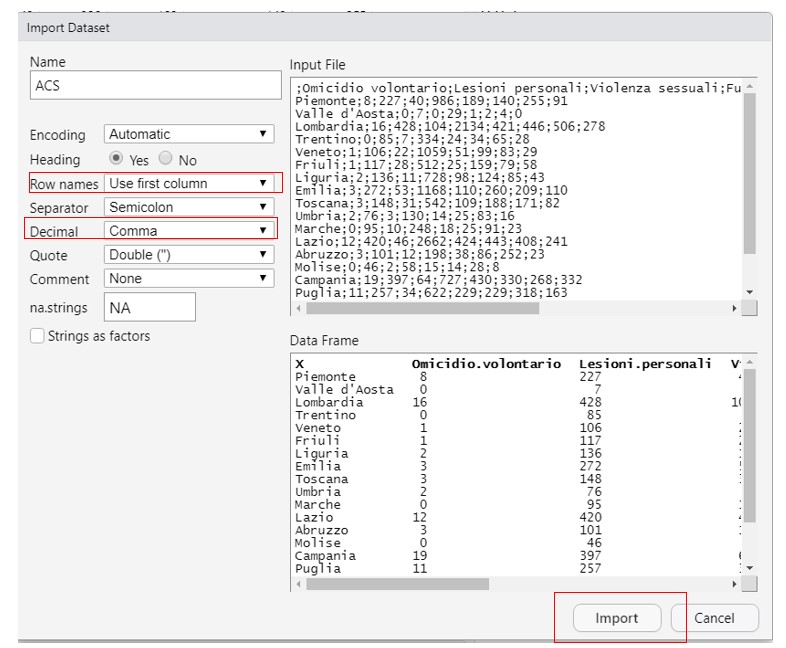
The last part of the module will be dedicated to the application of AC with the R software.
Van der Heijden, P. G. M. & de Leeuw, J. (1985). Correspondence analysis used complementary to loglinear analysis, Psychometrika, 50, pp. 429-447.
Le, S., Josse, J. & Husson, F. (2008). FactoMineR: An R Package for Multivariate Analysis. Journal of Statistical Software. 25(1). pp. 1-18.
Mineo, A. M. (2003). Una Guida all'utilizzo dell'Ambiente
Statistico R, http://cran.r-project.org/doc/contrib/Mineo-dispensaR.pdf.
Related training material
 Play Audio
Play Audio