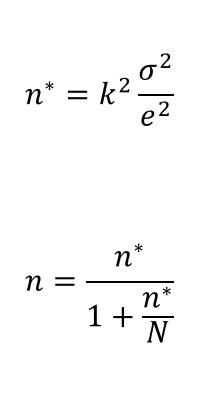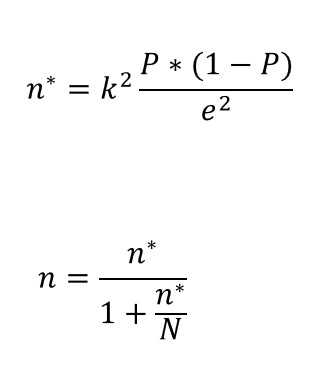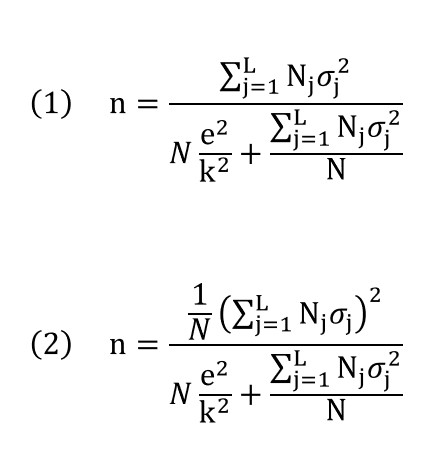|
Stichprobentheorie
Einleitung
Einleitung Click to read 
In der statistischen Analyse ist eine Grundgesamtheit (Population) eine Gruppe, für die wir einen Datensatz erstellen und einige Schlussfolgerungen ziehen wollen. Eine Erhebung ist ein Verfahren, mit dem wir die zu analysierenden Daten erhalten. Erhebungen können auf der Gesamtbevölkerung basieren (zensus- oder bevölkerungsbasiert), oder wir möchten eine repräsentative Teilmenge dieser Population auswählen. Diese Teilmenge wird als "Stichprobe" bezeichnet, wenn ihre Struktur dieselbe ist wie die der Grundgesamtheit. Daten aus Erhebungen, die eine Stichprobe heranziehen, werden als stichprobenbasiert bezeichnet.
Warum werden Datensätze in Form von Stichproben erhoben, anstatt die gesamte Bevölkerung zu untersuchen (Erhebungen auf der Grundlage von Volkszählungen)? Letztere sind für Zählungen und erschöpfende Untersuchungen notwendig, erfordern jedoch den Einsatz umfangreicher Ressourcen, was zu hohen Kosten führt.
Im Gegensatz dazu sind stichprobenartige Erhebungen geeignet, wenn die Bevölkerung homogen ist, da sie ein gutes Abbild der Bevölkerung darstellen. Außerdem sind sie die einzige Möglichkeit, wenn die Grundgesamtheit unendlich groß ist oder der Erhebungsprozess zu Informationszerstörungen führen kann. In jedem Fall sparen Stichproben Zeit und Kosten.
In der Praxis haben wir in der Regel nicht die Ressourcen, um bevölkerungsbezogene Studien durchzuführen, so dass die Alternative darin besteht, unsere Analyse auf Stichproben zu stützen. Wenn wir unsere Schlussfolgerungen auf Stichprobendaten stützen, bedeutet dies, dass es eine inhärente Fehlerspanne gibt, auf die sich mehrere Faktoren auswirken können.
Die Fehlermarge wird im Wesentlichen von drei Faktoren abhängen:
- Wie homogen die Daten in der Grundgesamtheit sind: Je heterogener die Daten sind, desto größer ist die Fehlermarge, wenn alle anderen Faktoren gleich bleiben.
- Der Stichprobenumfang: Je kleiner der Umfang, desto größer ist die Fehlermarge, wenn alles andere gleich bleibt.
- Das Stichprobenverfahren: abhängig von den Merkmalen Ihrer Daten
Bei (a) können wir nicht viel tun, aber bei den Punkten (b) und (c) gibt es einen gewissen Handlungsspielraum. Zu Punkt (c) über die angewandte Stichprobentechnik ist anzumerken, dass es eine große Vielfalt an verfügbaren Stichprobentechniken gibt, die wir anwenden können. Das nachstehende Diagramm zeigt diese Vielfalt in visueller Form:

Wir können die Fehlermarge unserer Schlussfolgerungen nur kontrollieren, wenn wir mit Zufallsstichproben arbeiten, und die am häufigsten verwendeten Stichprobenverfahren sind die einfache Zufallsstichprobe und die geschichtete Zufallsstichprobe.
Probenahmetechniken
Einfache Zufallsstichprobe Click to read 
Die einfache Zufallsstichprobe ist das elementarste Stichprobenverfahren, das auf einer Zufallsauswahl der untersuchten Beobachtungen beruht. Sie besteht darin, ausgehend von einer Auflistung der Einheiten der Grundgesamtheit, n dieser Einheiten zufällig auszuwählen. Aber selbst bei dieser einfachen Technik können einige Besonderheiten des Zufallsauswahlverfahrens festgelegt werden. So kann beispielsweise entschieden werden, ob die Stichprobe mit oder ohne Zurücklegen durchgeführt werden soll. Wird die Stichprobe mit Zurücklegen durchgeführt, bedeutet dies, dass jede Einheit, die nach dem Zufallsprinzip als Teil der Stichprobe ausgewählt wurde, nach jeder Ziehung wieder in die Grundgesamtheit aufgenommen wird. Dies bedeutet natürlich, dass eine Einheit mehr als einmal in die Stichprobe aufgenommen werden kann, aber es garantiert, dass die Bedingungen, unter denen die einzelnen Ziehungen stattfinden, gleich und konstant sind und die Ergebnisse der einzelnen Ziehungen unabhängig voneinander sind.
Im Gegensatz dazu wird bei einer einfachen Zufallsstichprobe ohne Zurücklegen jede Einheit nur einmal beprobt, aber wir können nicht garantieren, dass die Bedingungen entlang der Auswahlziehungen konstant sind. Stichproben mit und ohne Zurücklegen können bei kleinen Populationen zu sehr unterschiedlichen Ergebnissen führen. Sie sind nur dann gleichwertig, wenn die Größe der Grundgesamtheit (N) sehr groß ist.
Geschichtete Zufallsstichprobe Click to read 
In manchen Fällen werden die Beobachtungen natürlich auf der Grundlage gemeinsamer Merkmale gruppiert. So werden beispielsweise Daten über die Lohnverteilung nach dem Wirtschaftszweig der Arbeitnehmer, ihrem Geschlecht oder ihrer Wohnregion gruppiert. Schichten werden als Teile der relevanten Population definiert, die eine hohe interne Homogenität aufweisen, auch wenn zwischen den Schichten eine große Variabilität besteht. Die geschichtete Stichprobe nutzt diese Gruppierung der Beobachtungen und wählt nach dem Zufallsprinzip eine Anzahl von Einheiten in jeder Schicht L (nL ) aus, so dass sich der Gesamtstichprobenumfang durch Addition der in jeder Schicht beprobten Elemente ergibt. Es gibt mehrere Kriterien für die Aufteilung des Gesamtstichprobenumfangs auf die Schichten, von denen die folgenden die häufigsten sind:
- Disproportional: gleiche Stichprobengröße in jeder Schicht
- Proportional: der Anteil der Stichprobenmitglieder entspricht dem Anteil der Bevölkerungsmitglieder in jeder Schicht
- Optimal: proportional zur Größe und Heterogenität (Varianz) der einzelnen Schichten
Unter den gleichen Bedingungen und mit den gleichen Anforderungen an Präzision und Konfidenzintervall können wir bestätigen, dass geschichtete Stichproben im Allgemeinen einen geringeren Stichprobenumfang erfordern als einfache Stichproben. Auf Fragen im Zusammenhang mit der Berechnung des Stichprobenumfangs wird im nächsten Punkt eingegangen.
Berechnung des optimalen stichprobenumfangs
Berechnung des optimalen stichprobenumfangs Click to read 
Die goldene Regel für den Zusammenhang zwischen dem Stichprobenumfang und der Genauigkeit unserer Schätzungen lautet, dass die Fehlermarge umso geringer ist, je größer der Stichprobenumfang ist, wenn alle anderen Faktoren gleich bleiben. Die Beschaffung statistischer Daten, selbst wenn sie in Form einer Stichprobe erfolgt, kann jedoch kostspielig sein, und manchmal fehlen uns die Mittel für große Stichproben. Folglich gibt es eine Kompromisslösung, die den optimalen (minimalen) Stichprobenumfang festlegt, den wir angesichts unserer Anforderungen an die Genauigkeit (Fehlermarge) und das Vertrauen in unsere Schätzungen sowie die Heterogenität (Varianz) der relevanten Variablen in der Grundgesamtheit benötigen.
|
Regel: Je größer der Stichprobenumfang, desto genauer die Schätzung
|
|
 |
|
Lösung für eine einfache Stichproboben Click to read 
Nehmen wir zunächst an, dass wir mit unserer Stichprobe den Mittelwert der Grundgesamtheit für eine kontinuierliche Variable schätzen wollen und dass unsere Stichprobe anhand einer einfachen Zufallsstichprobe ausgewählt wird. Die Formeln, die wir anwenden müssen, sind die folgenden:
Die Konstante 𝑘 stammt aus einer Normalverteilung und wird größer, wenn wir das gewünschte Konfidenzintervall erhöhen, und das Symbol 𝑒 steht für die Fehlermarge, die wir anzunehmen bereit sind. Zusätzlich müssen wir eine Annahme über die Homogenität der Variablen in der Grundgesamtheit treffen. Dies bedeutet, dass wir einen realistischen Wert (der in der Regel aus einer früheren Studie stammt) für die Varianz der Population σ 2 festlegen müssen..
In diesen Gleichungen ist n∗ die Lösung für eine einfache Zufallsstichprobe mit Zurücklegen, 𝑛 ist die Lösung für eine einfache Zufallsstichprobe ohne Zurücklegen und N ist die Größe der Grundgesamtheit. Generell gilt  , und beide Lösungen konvergieren, wenn N sehr groß ist. , und beide Lösungen konvergieren, wenn N sehr groß ist.
Wenn wir daran interessiert sind, den Anteil (P) der Einheiten in einer Grundgesamtheit zu schätzen, die ein bestimmtes Merkmal aufweisen, lauten die Ausdrücke, die erforderlich sind, um den optimalen Stichprobenumfang für dieses Stichprobenverfahren zu finden, wie folgt:
Auch hier stammt die Konstante 𝑘 aus einer Normalverteilung und wird größer, wenn wir das gewünschte Konfidenzintervall erhöhen, und der Term 𝑒 steht für die Fehlermarge, die wir bereit sind, anzunehmen. In diesem Fall müssen wir eine Annahme über den Wert von P*(1-P) machen, der die Varianz einer binären (ja/nein) Variable ist. Die übliche Lösung besteht darin, P=1-P=0,5 anzunehmen, so dass P*(1-P)=0,25 seinen Maximalwert annimmt.
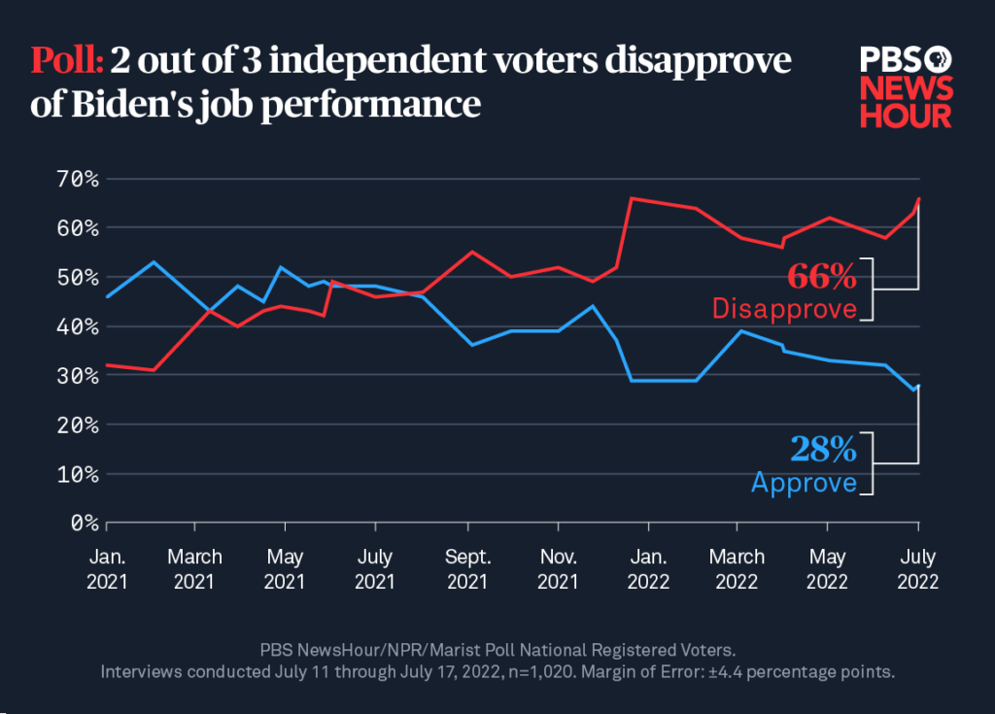
Wir können diese Technik anhand eines praktischen Beispiels veranschaulichen, wie Stichprobengrößen bestimmt werden und wie die Anwendung von R uns dabei helfen kann: Der Public Broadcasting Service (PBS) in den USA schätzt regelmäßig den Prozentsatz der Bürger:innen, welche die Arbeit des US-amerikanischen Präsidenten gutheißen oder ablehnen. Im Fall von US-Präsident Joe Biden werden diese Umfragen seit Januar 2021 durchgeführt. Die folgende Grafik zeigt die Entwicklung der Schätzungen:
Bei einer kürzlich durchgeführten Umfrage in dieser Reihe wollte PBS Schätzungen mit einem Konfidenzniveau von 99 % erhalten, war bereit, eine Fehlermarge von ±4,4 % in Kauf zu nehmen, ging vom ungünstigsten Fall aus (übliche Lösung) und nahm an, dass der Prozentsatz der Befürworter (P) gleich dem Prozentsatz der Nichtbefürworter (1-P) ist. Wie viele Bürger:innen müssten unter diesen Bedingungen in die Stichprobe aufgenommen werden? Die oben dargestellten Gleichungen können in der Sprache R implementiert werden, um eine Lösung zu finden.
Zunächst müssen wir die erforderlichen Pakete installieren und laden:

Später können wir diesen optimalen Stichprobenumfang durch Aufruf der Funktion "sample.size.prop" im Paket ermitteln. Diese Funktion ermöglicht eine Stichprobenziehung mit oder ohne Zurücklegen, obwohl es in der Praxis keine Unterschiede zwischen den Lösungen dieser beiden Alternativen gibt, da die Grundgesamtheit (N), aus der die Stichproben gezogen werden, sehr groß ist (wir können willkürlich annehmen, dass N=200.000.000). Die folgenden Codeteile berechnen die jeweiligen Lösungen für eine Stichprobe ohne und mit Zurücklegen:
Die in beiden Fällen als Lösung eine Stichprobengröße von etwa 1.000 Einheiten findet.
Lösung für geschichtete Stichproben Click to read 
In diesem Abschnitt werden die Formeln für die Berechnung des Stichprobenumfangs bei geschichteten Stichproben ausführlich erläutert. Der Einfachheit und Klarheit halber konzentrieren wir uns nur auf den Fall der Schätzung eines Populationsmittelwerts und bieten die beiden häufigsten Lösungen an, die den Fällen der proportionalen (1) und der optimalen Verteilung (2) entsprechen:
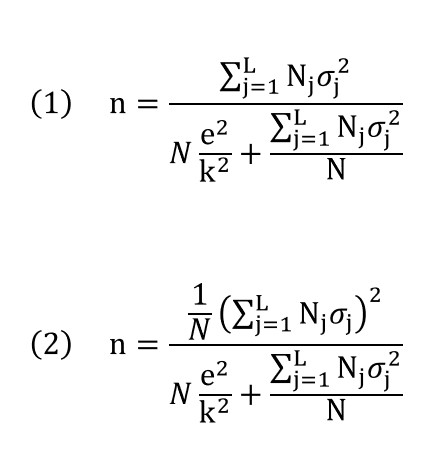 |
Wie bereits erwähnt, entspricht die Formel in beiden Fällen der Schätzung des Populationsmittelwerts für eine kontinuierliche Variable mit einer geschichteten Stichprobe ohne Zurücklegen. In diesen Ausdrücken steht Nj ür die Größe der Schicht j und σj2 für die Varianz der Variablen in dieser Schicht.
Ähnlich wie bei den Lösungen für einfache Zufallsstichproben können wir anhand eines praktischen Beispiels in der Sprache R veranschaulichen, wie der optimale Stichprobenumfang bei geschichteten Stichproben berechnet wird.
Angenommen, ein Wohlfahrtsverband führt eine Stichprobenerhebung durch, um die jährlichen Spenden seiner Mitglieder zu untersuchen, die je nach Alter in drei verschiedene Gruppen mit jeweils 100, 700 und 200 Mitgliedern eingeteilt sind. Aus einer Pilotstudie weiß die Wohltätigkeitsorganisation, dass die jeweiligen Standardabweichungen (σj) bei den jährlichen Spenden in jeder Gruppe 6 €, 30 € und 12 € betragen. Es soll der Mindeststichprobenumfang ermittelt werden, der erforderlich ist, um die mittlere jährliche Spende zu schätzen, wobei eine Fehlermarge von 2 € und ein Konfidenzniveau von 95 % angesetzt werden.
Die folgenden Codezeilen berechnen den optimalen Stichprobenumfang und bieten die Lösungen für den Fall einer proportionalen und optimalen Verteilung, indem sie die Funktion "stratasize" aus dem Paket "samplingbook" in R aufrufen:
 |
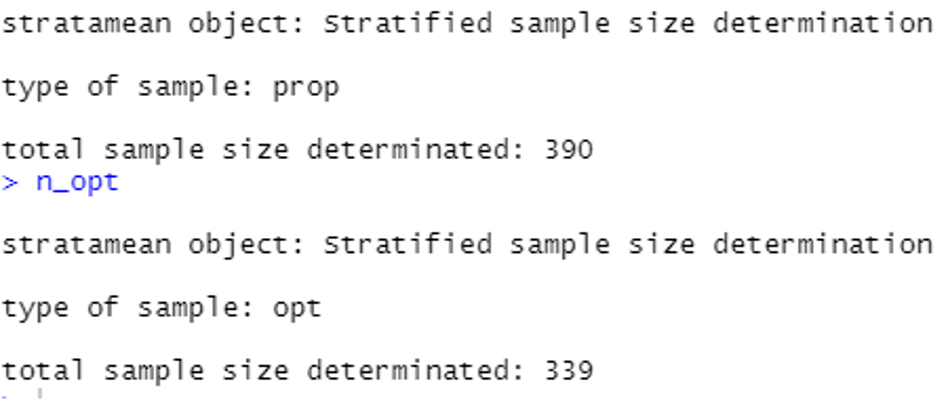
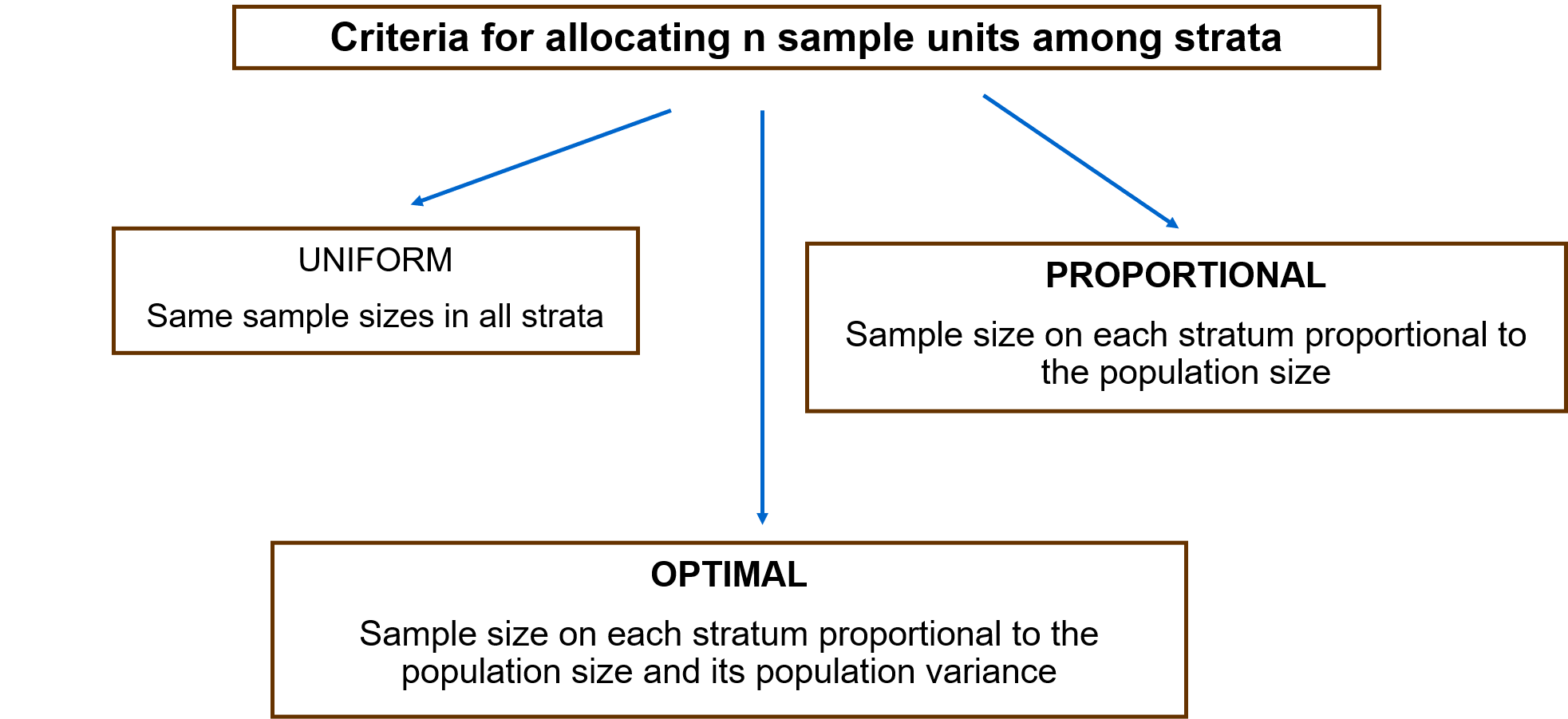
Die entsprechenden Lösungen sind 390 und 339 Einheiten, wie im Folgenden beschrieben:
Schließlich können wir uns fragen, welcher dieser beiden Stichprobenumfänge auf die Schichten aufgeteilt werden soll. Dies kann durch den Aufruf der Funktion "stratasamp" im selben Paket erfolgen:
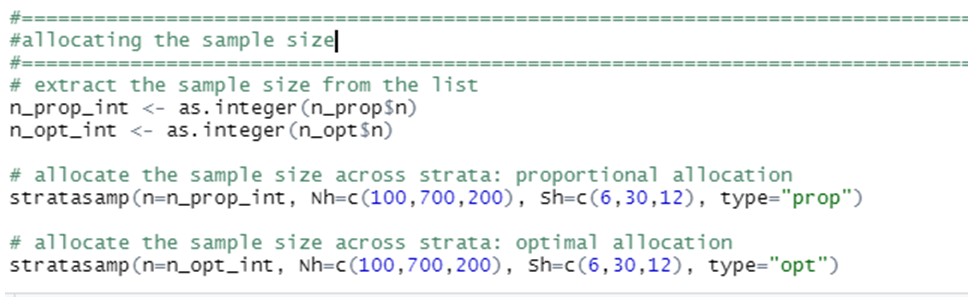
Die Lösungen dazu lauten:

|