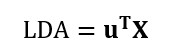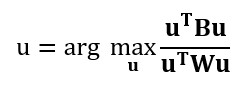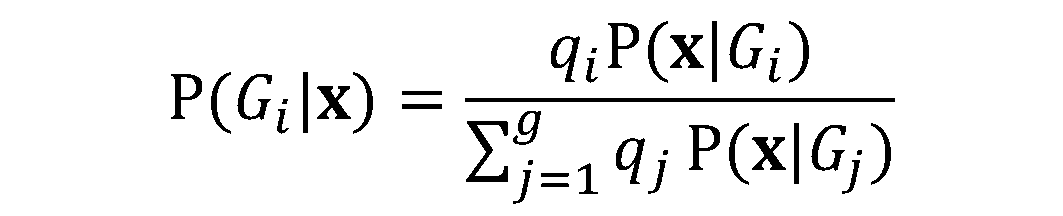DataScience Training
Keywords
Analisi discriminante, classificazione, R, analisi bayesiana
Objectives/goals:L'obiettivo di questo modulo è introdurre e spiegare le basi dell'analisi discriminante lineare (LDA).
Alla fine di questo modulo sarai in grado di:
- Identificare le situazioni in cui LDA può essere utile
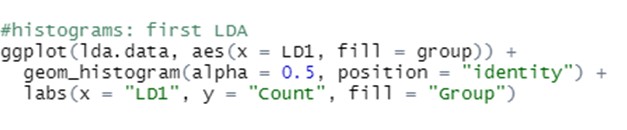
- Calcolare le funzioni LDA
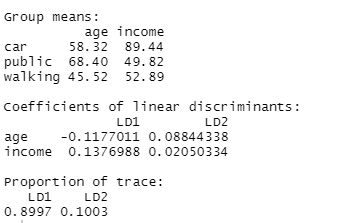
- Interpretare i risultati prodotti da LDA descrittivo e predittivo
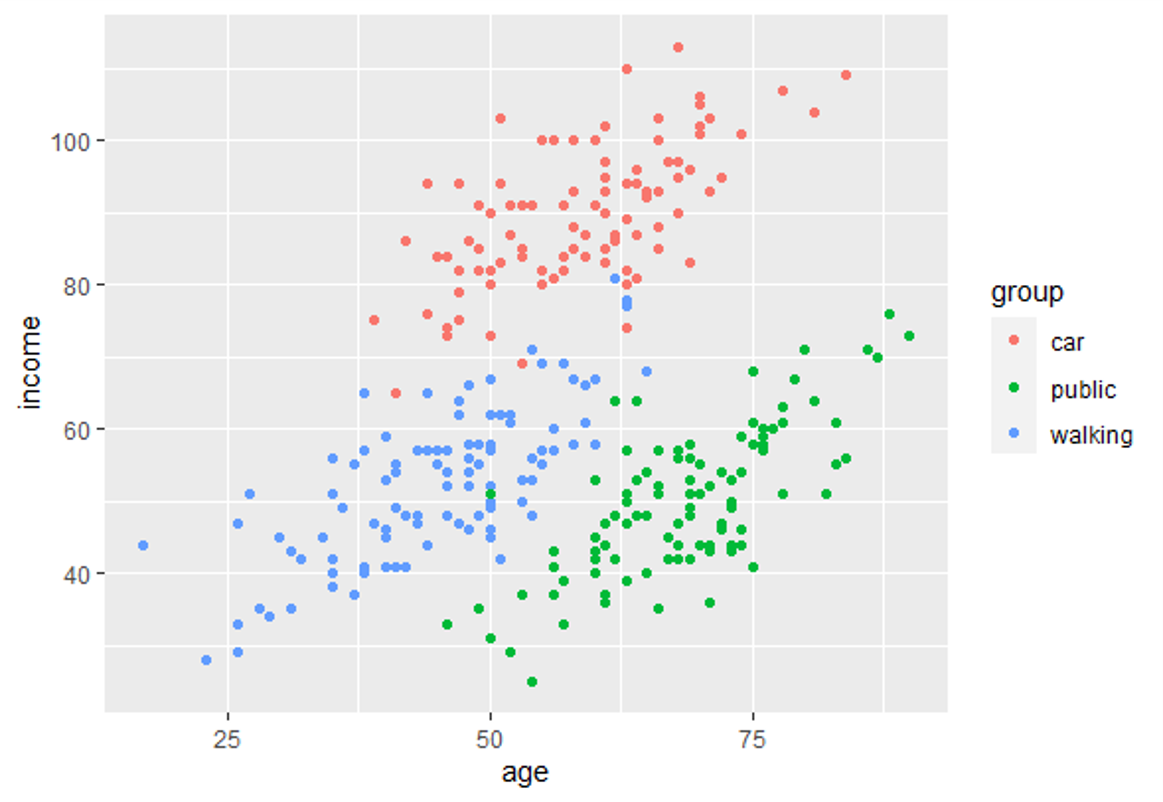
In questo modulo di formazione verrai introdotto all'uso dell'analisi discriminante lineare (LDA). LDA è un metodo per trovare combinazioni lineari di variabili che meglio separa le osservazioni in gruppi o classi, ed è stato originariamente sviluppato da Fisher (1936).
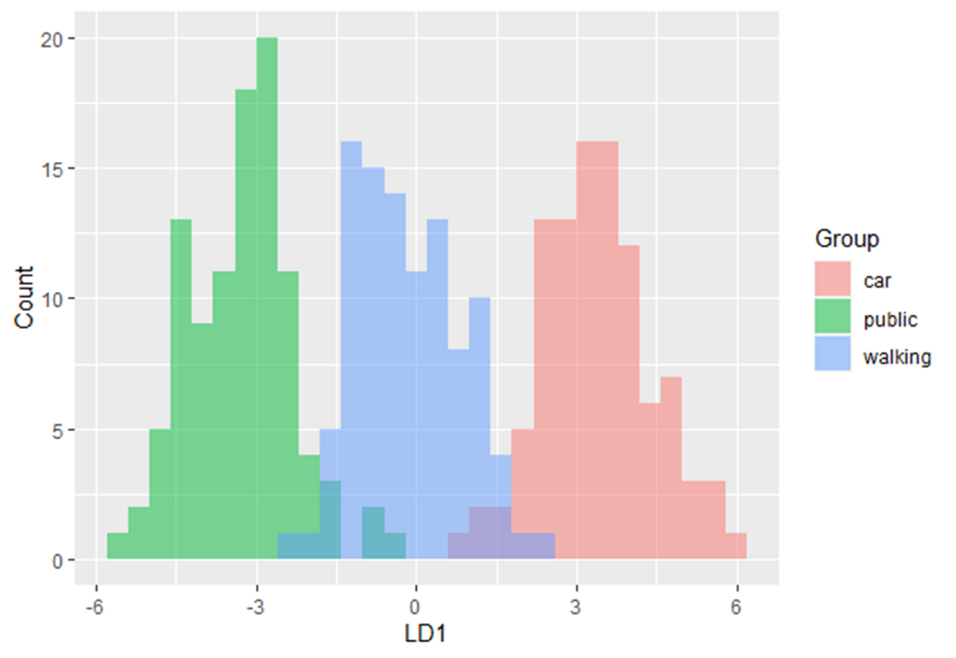
Questo metodo massimizza il rapporto tra la varianza tra classi e la varianza all'interno della classe in un particolare set di dati. In questo modo, la variabilità tra gruppi è massimizzata, il che si traduce in massima separabilità.
LDA può essere utilizzato con scopi puramente di classificazione, ma anche con obiettivi predittivi.
Boedeker, P., & Kearns, N. T. (2019). Linear discriminant analysis for prediction of group membership: A user-friendly primer. Advances in Methods and Practices in Psychological Science, 2, 250-263.
Related training material
 Riprodurre l’audio
Riprodurre l’audio