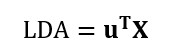DataScience Training
Keywords
analiza discriminant, clasificare, R, analiză bayesiană
Objectives/goals:Obiectivul acestui modul este de a introduce și explica elementele de bază ale analizei discriminante liniare (LDA).
La sfârșitul acestui modul vei fi capabil să:
- Identificați situațiile în care LDA poate fi utilă
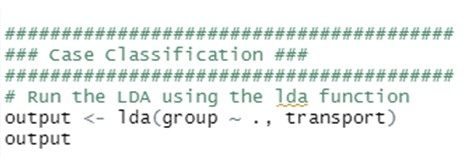
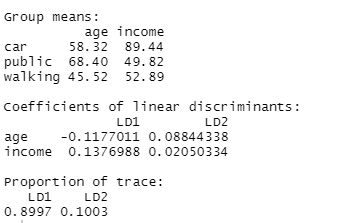
- Calculați funcțiile LDA
- Interpretarea rezultatelor produse de LDA descriptiv și predictiv
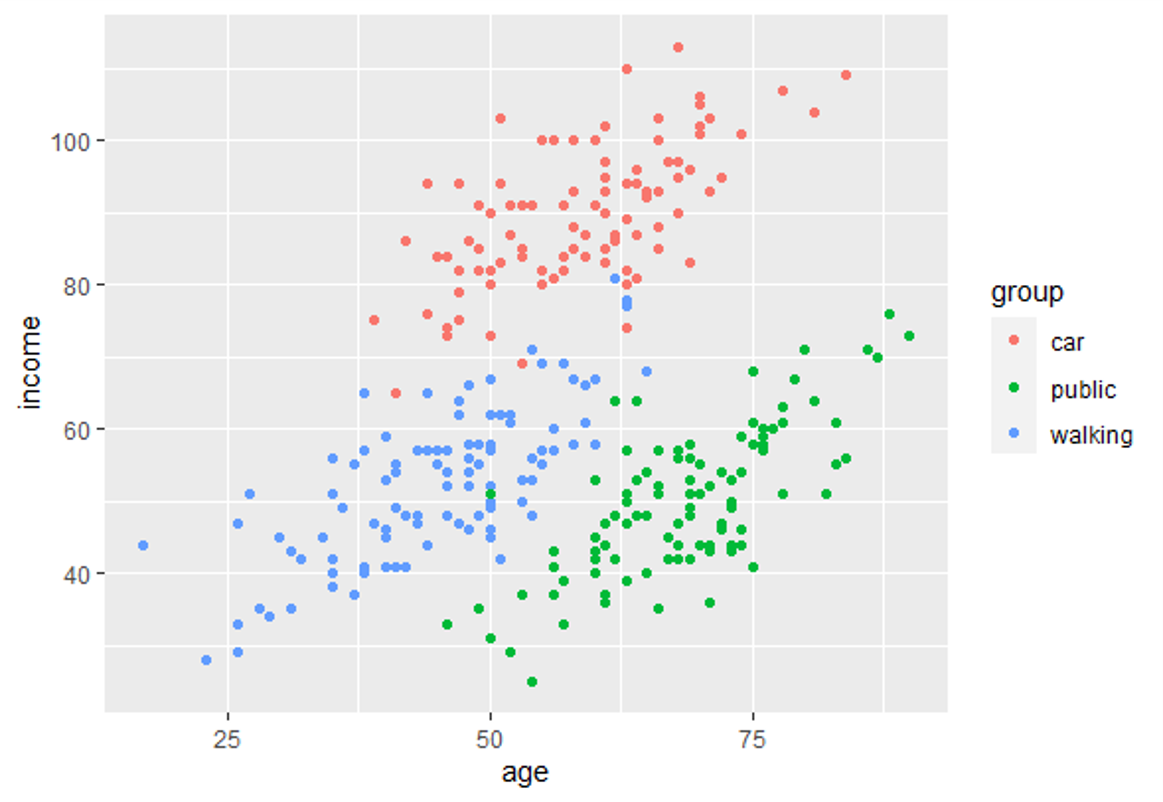
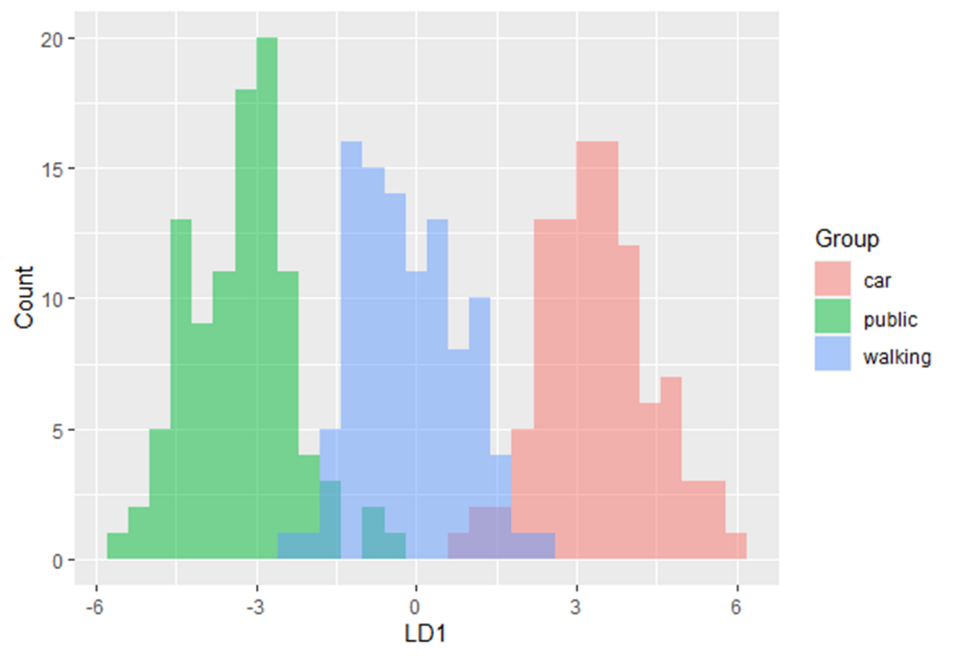
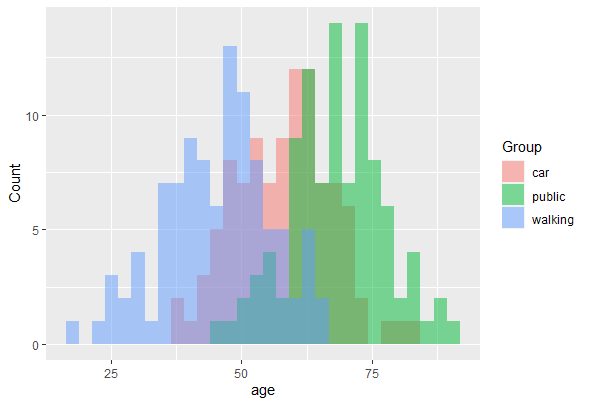
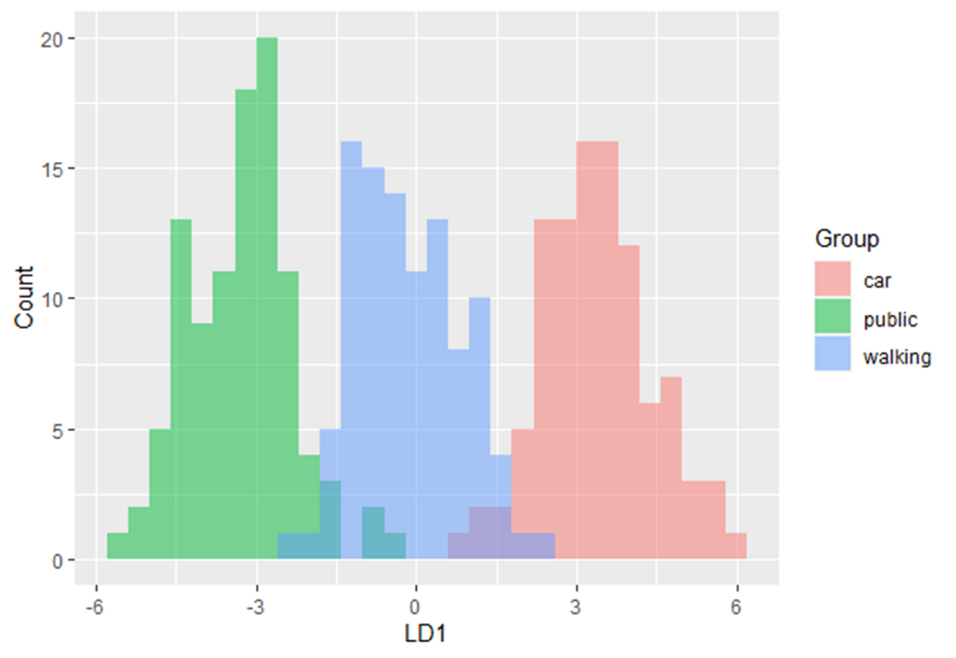
În acest modul de instruire veți fi introdus în utilizarea analizei discriminante lineare (LDA). LDA este o metodă de găsire a combinațiilor liniare de variabile care separă cel mai bine observațiile în grupuri sau clase și a fost dezvoltată inițial de Fisher (1936).
Această metodă maximizează raportul dintre variația dintre clase și varianța în interiorul clasei în orice anumit set de date. Făcând acest lucru, variabilitatea între grupuri este maximizată, ceea ce are ca rezultat separabilitatea maximă.
LDA poate fi folosit cu scopuri pur de clasificare, dar și cu obiective predictive.
Boedeker, P., & Kearns, N. T. (2019). Linear discriminant analysis for prediction of group membership: A user-friendly primer. Advances in Methods and Practices in Psychological Science, 2, 250-263.
Related training material
 Redare audio
Redare audio