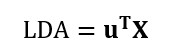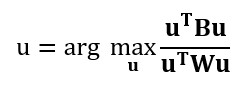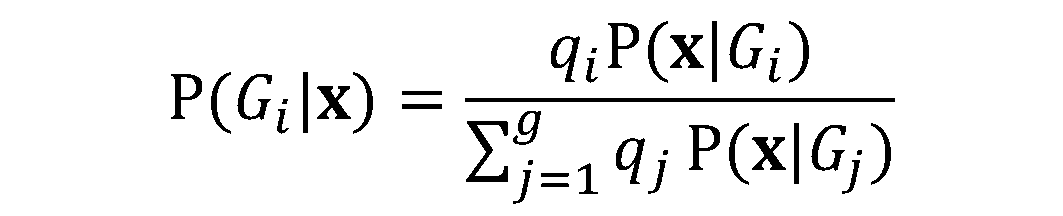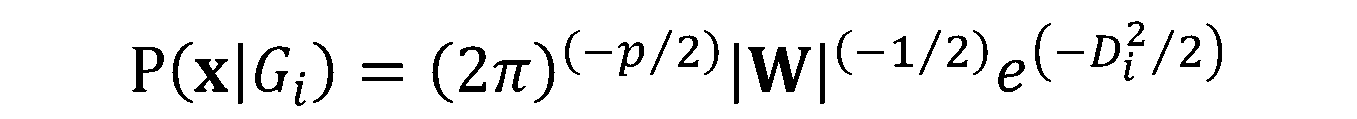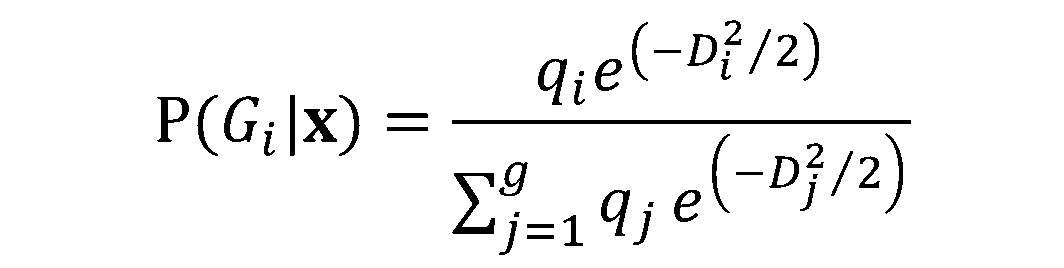DataScience Training
Keywords
Diskriminanzanalyse, Klassifizierung, R, Bayes'sche Analyse
Objectives/goals:Ziel dieses Moduls ist es, die Grundlagen der linearen Diskriminanzanalyse (LDA) vorzustellen und zu erklären.
Am Ende dieses Moduls werden Sie in der Lage sein:
- Situationen zu identifizieren, in denen LDA nützlich sein kann
- Berechnung von LDA-Funktionen
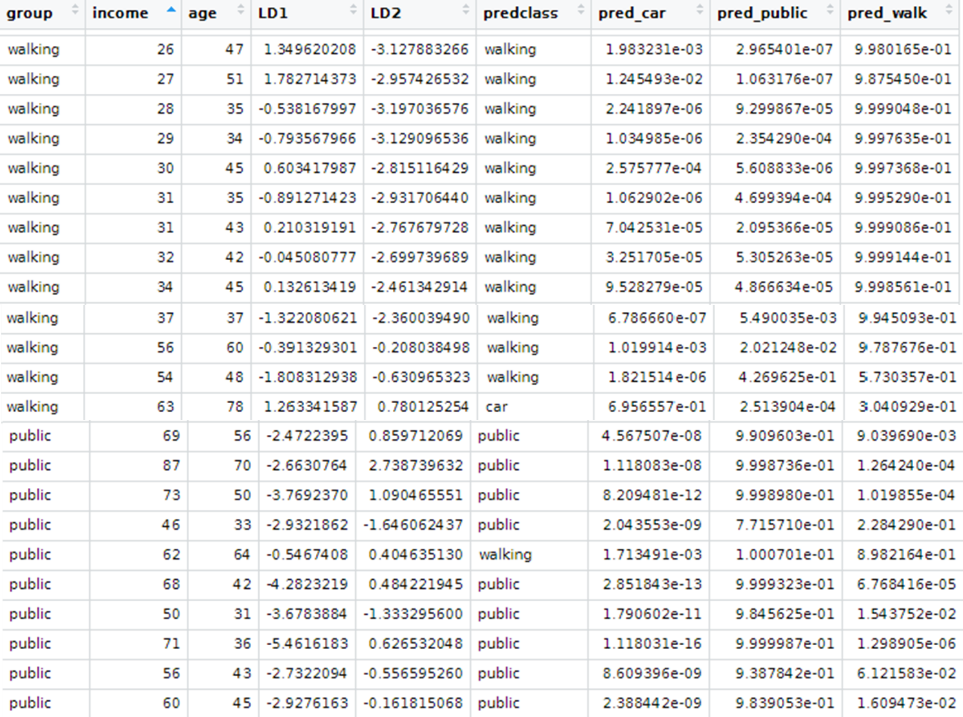
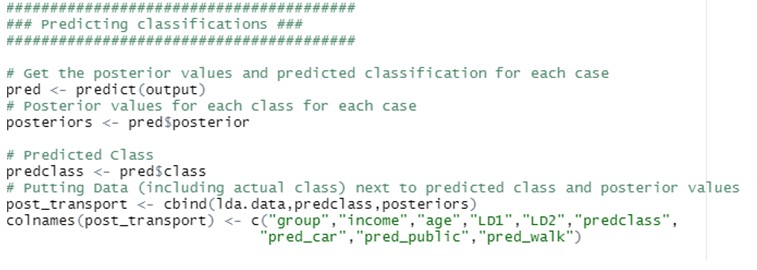
- Interpretion der Ergebnisse der deskriptiven und prädiktiven LDA
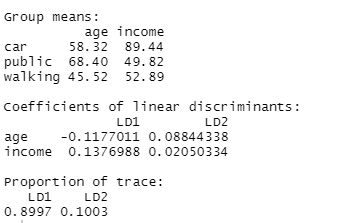
In diesem Schulungsmodul lernen wir die Anwendung der Diskriminanzanalyse (linear discriminant analysis bzw. LDA) eingeführt. LDA ist eine Methode zum Berechnen von Linearkombinationen von Variablen, die die Beobachtungen am besten in Gruppen oder Klassen einteilen, und wurde ursprünglich von Fisher (1936) entwickelt.
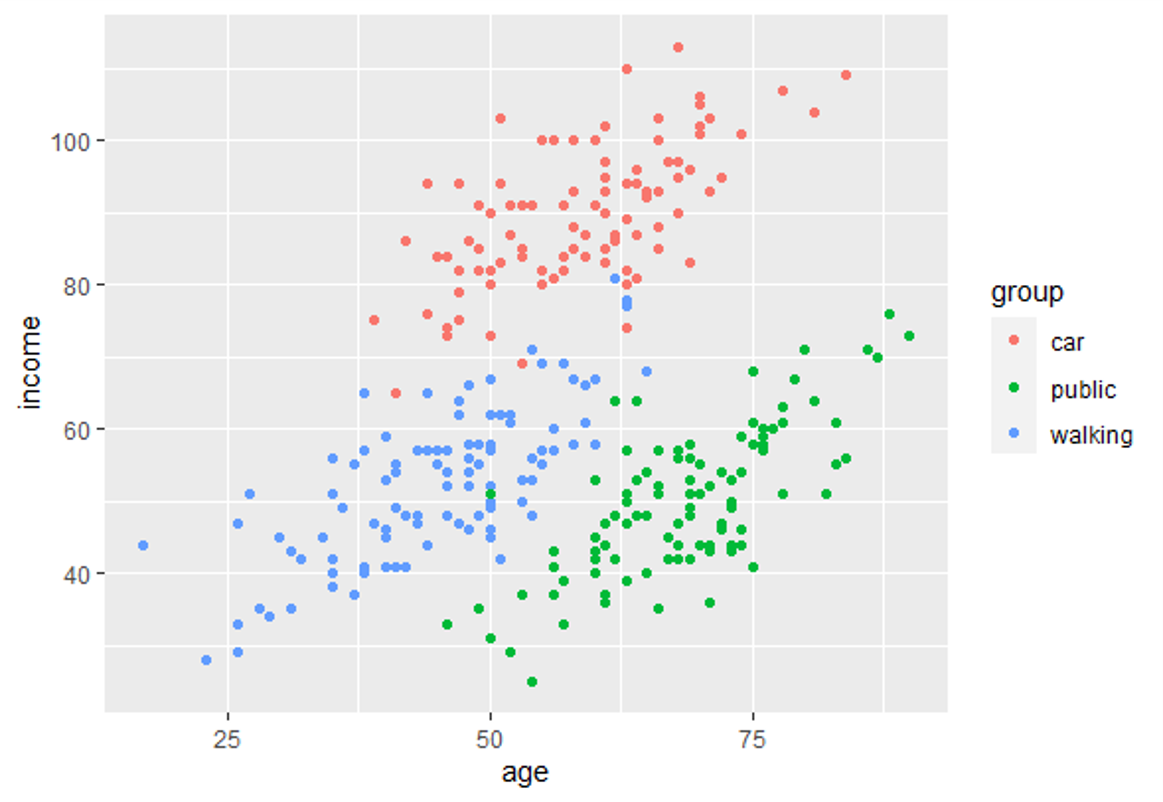
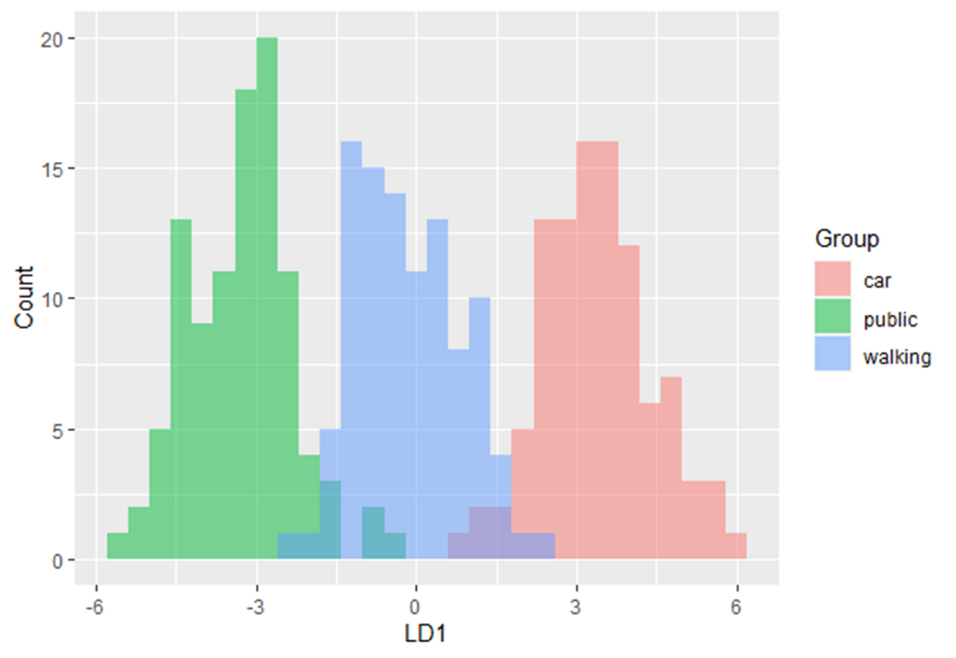
Diese Methode maximiert das Verhältnis der Varianz zwischen den Klassen zur Varianz innerhalb der Klassen in einem bestimmten Datensatz. Auf diese Weise wird die Variabilität zwischen den Gruppen maximiert, was zu einer maximalen Trennbarkeit führt.
LDA kann für reine Klassifizierungszwecke, aber auch für die Vorhersage von Klassenzugehörigkeiten eingesetzt werden.
Boedeker, P., & Kearns, N. T. (2019). Linear discriminant analysis for prediction of group membership: A user-friendly primer. Advances in Methods and Practices in Psychological Science, 2, 250-263.
Related training material