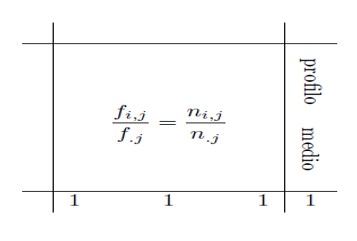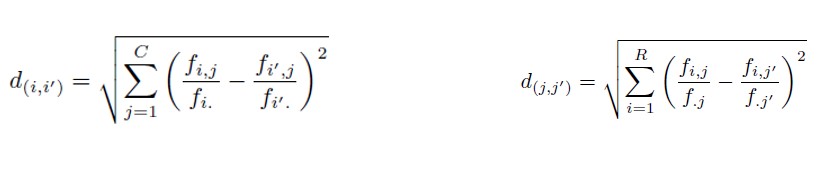|
Korrespondenzanalyse (Correspondence Analysis)
Einleitung
Korrespondenzanalyse (CA) Click to read 
Die Korrespondenzanalyse (CA) ist ein statistisches Verfahren zur Analyse mehrdimensionaler Daten. Es handelt sich um eine multivariate Technik, die Assoziationsmuster zwischen qualitativen Variablen analysiert.
Qualitative Variablen sind Variablen, die nicht durch Zahlen, sondern durch Modalitäten dargestellt werden, z. B.: Geschlecht, Bildungsniveau, Familienstand usw.
Da in der Korrespondenzanalyse qualitative Variablen verwendet werden, müssen wir zuerst Kontingenzmatrizen erstellt werden.
Die Elemente der Kontingenzmatrix geben an, wie häufig die Merkmale zweier unterschiedlicher Größen gleichzeitig auftreten.
Ziel der Korrespondenzanalyse Click to read 
Das Hauptziel der Korrespondenzanalyse ist die Analyse der Beziehungen zwischen einer Reihe von qualitativen Variablen, die an einem Kollektiv von statistischen Einheiten beobachtet werden. Dies geschieht durch die Identifizierung eines "optimalen" Raums, d. h. einer kleinen Dimension, die die Synthese der in den ursprünglichen Daten enthaltenen Strukturinformationen darstellt.
Im Wesentlichen werden wir eine Reihe von latenten Variablen (oder Faktoren) ermitteln. Diese latenten Variablen sind eine Kombination aus den ursprünglichen Variablen und drücken einige Konzepte aus, die in der Realität nicht direkt beobachtbar sind, sondern das Ergebnis der Messung einer Reihe von Variablen sind.
Die Annahme der Korrespondenzanalyse Click to read 
Bei der Korrespondenzanalyse dürfen die verwendeten Variablen nicht unabhängig sein, d. h. die Werte der einen Variable müssen die Werte der anderen beeinflussen.
Vor der Durchführung einer Korrespondenzanalyse ist es notwendig, den Grad der gegenseitigen Abhängigkeit zwischen den betrachteten Merkmalen festzustellen: wenn sie unabhängig sind, ist es möglicherweise nicht sinnvoll, nach den Korrespondenzen zwischen ihnen zu suchen.
Zu diesem Zweck ist es notwendig, den Chi-Quadrat-Test anzuwenden, mit dem eventuelle Abhängigkeitsbeziehungen zwischen den qualitativen Variablen bewertet werden.
Der Test beginnt mit der Nullhypothese, wonach die beiden Variablen unabhängig sind. Die Alternativhypothese lautet, dass die beiden Variablen einen gewissen Grad an Interdependenz aufweisen.
Wenn die Testergebnisse einen p-Wert < 0,05 ergeben, kann die Nullhypothese verworfen werden und die beiden Variablen werden als voneinander abhängig betrachtet.
Wir können daher mit der Korrespondenzanalyse fortfahren.
Korrespondenzanalyse
Kontingenztabellen Click to read 
Die Kontingenztabellen enthalten die gemeinsamen Häufigkeiten der Variablenwerte. Bei zwei qualitativen Variablen X und Y enthält die entsprechende Kontingenztabelle, wie oft ein bestimmter Modus der Variablen X mit einem bestimmten Modus der Variablen Y auftritt.
Die Korrespondenzanalyse ermöglicht es, das Phänomen sowohl im Raum der Zeilen als auch im Raum der Spalten darzustellen.
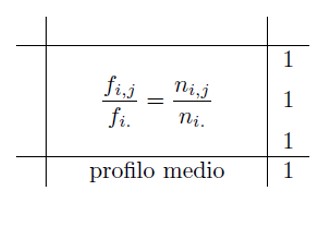
Zu diesem Zweck müssen die Zeilen- und Spaltenprofilmatrizen konstruiert werden:
- Entweder: Division der absoluten Häufigkeiten durch die entsprechenden Randhäufigkeiten der Zeilen bzw. Spalten;
- Oder: Division der relativen Häufigkeiten (d. h. der absoluten Häufigkeiten geteilt durch die Gesamtzahl der Stichprobe) durch die entsprechenden relativen Randhäufigkeiten der Zeilen bzw. Spalten.
|
Zeilenprofilmatrix
|
Spaltenprofilmatrix |
 |
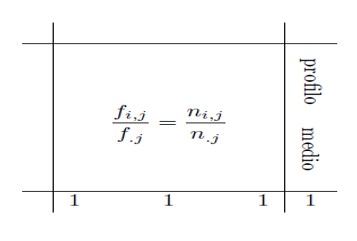 |
Abstände zwischen Profilen Click to read 
Schließlich werden wir die Abstände zwischen den Profilen berechnen, um festzustellen, ob die Modalitäten ähnlich sind oder nicht, und ob sie voneinander entfernt sind oder nicht, d. h. ob die Profile einander ähneln oder nicht.
Es gibt zwei Arten von Abständen: den euklidischen Abstand und den Chi-Quadrat-Abstand.
- Der euklidische Abstand begünstigt größere Abstände über kleinere Abstände und wird berechnet, indem die Differenz zwischen den relativen Häufigkeiten gebildet und dann quadriert wird.
- Der Chi-Quadrat-Abstand bevorzugt die geringsten Abstände, da er die Anzahl der Zeilen berücksichtigt. Er wird berechnet, indem die Differenz der Häufigkeiten in Bezug auf den Rahmen mit dem Kehrwert des Randes der Zeile (oder Spalte) gewichtet wird.
Eine Fallstudie
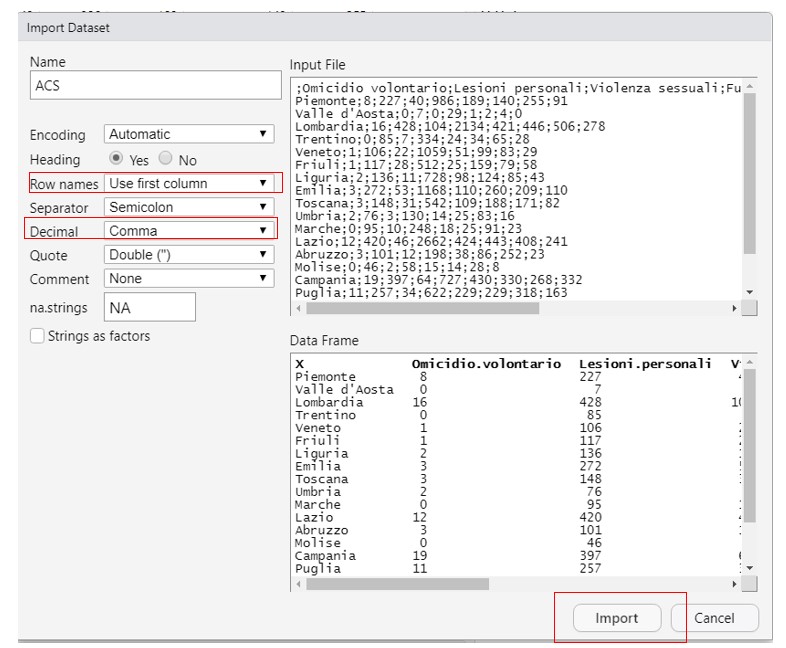
Importieren des Datensatzes Click to read  Chi-Quadrat-Test Click to read 
|
Der Chi-Quadro-Test ist notwendig, um zu überprüfen, ob die Variablen nicht unabhängig sind. In diesem Fall sind die italienischen Regionen und die in Italien begangenen Straftaten unsere Variablen.
Die Nullhypothese des Tests lautet: ''Die Variablen sind unabhängig''
|
|
| |
|
 |
|
|
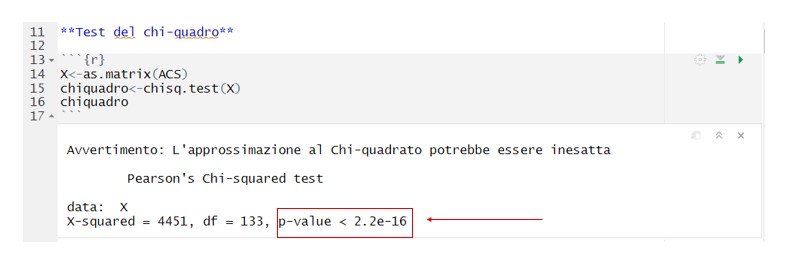
Der p-Wert hilft uns dabei, die Nullhypothese zurückzuweisen oder nicht zurückzuweisen.
Bei einem Alpha= 5% ist der p-Wert: 2,2e-16.
Da der p-Wert unter 5%, d. h. bei 0,05, liegt, wird die Nullhypothese abgelehnt, so dass die beiden Variablen als in gewissem Maße voneinander abhängig angesehen werden.
|
|
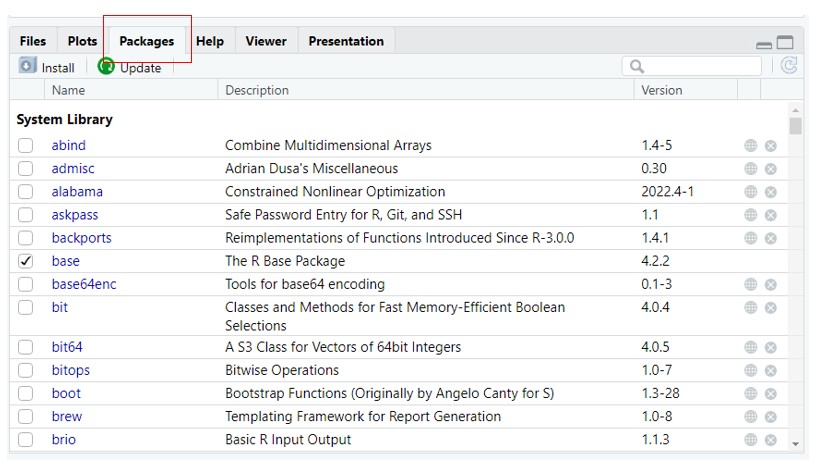
Korrespondenzanalyse in R Click to read 
Für die CA bietet R ein Paket namens FactoMineR.
Zuerst müssen wir das FactoMineR-Paket installieren.

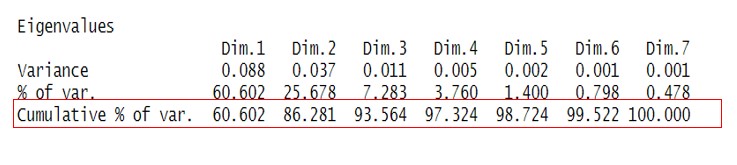 |
In Anbetracht des Ziels der Korrespondenzanalyse, die erklärte Trägheit zu beobachten, können wir sehen, auf welche Größe das Phänomen reduziert wird.
Wir sehen, dass die erste Dimension allein etwa 60 % der Gesamtvariabilität der Daten erklärt.
|
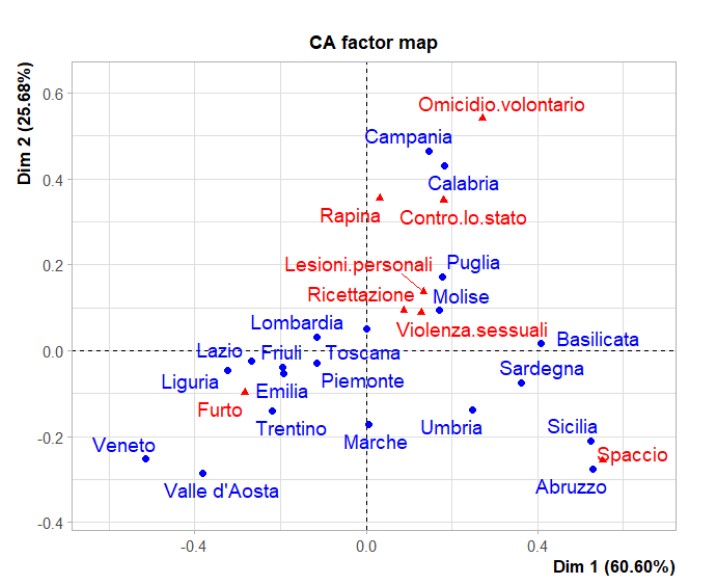
| Das gemeinsame zweidimensionale Diagramm der Einzelvariablen stellt grafisch dar, wie die Werte der beiden Variablen entlang der durch die neu extrahierten Dimensionen geschaffenen Achsen angeordnet sind. |
 |
Zusammenfassend
Zusammenfassend Click to read  |