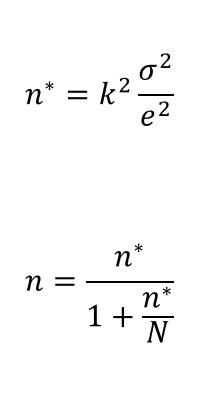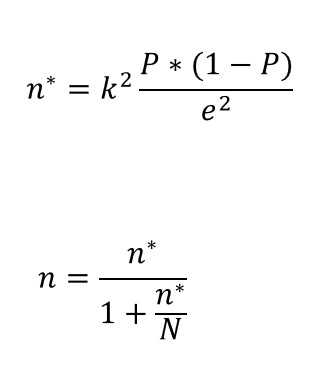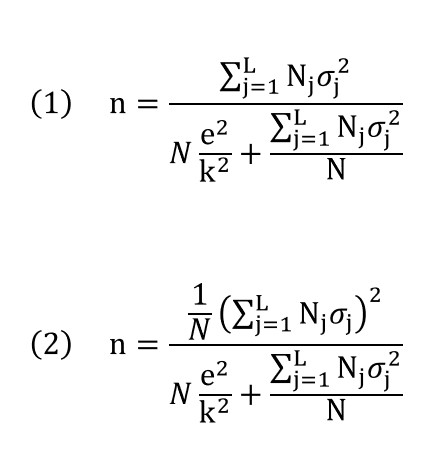|
Teoria Eșantionării
Introducere
Introducere Click to read 
În analiza statistică, o populație este un set de date pentru care dorim să tragem anumite concluzii. Un sondaj este o procedură prin care obținem datele care urmează să fie analizate. Sondajele se pot baza pe întreaga populație (bazate pe recensământ) sau am putea dori să selectăm un subgrup reprezentativ al acestei populații. Acest subgrup este definit drept "eșantion" dacă structura sa reflectă aceeași structură ca și în cazul populației, iar datele colectate în urma sondajelor se numesc ”date bazate pe eșantion”.
De ce să colectezi seturi de date sub forma unui eșantion în loc să investighezi întreaga populație (anchete bazate pe recensământ)? Anchetele bazate pe recensământ sunt necesare în cazul cercetărilor de numărare și al cercetărilor aprofundate, dar necesită utilizarea unor resurse uriașe, ceea ce duce la costuri ridicate. Dimpotrivă, anchetele pe bază de eșantion sunt adecvate în cazul în care populația este omogenă, deoarece acestea vor constitui o bună reprezentare a populației. În plus, acestea sunt singura opțiune atunci când populația este infinită și se află în proces de distrugere a informațiilor. În orice caz, eșantioanele economisesc timp și costuri.
În termeni practici, în mod normal, nu dispunem de resursele necesare pentru a efectua studii bazate pe recensământ (populație), astfel încât alternativa este de a ne baza analiza pe eșantioane. Bazarea concluziilor noastre pe date din eșantioane, implică faptul că va exista o marjă de eroare implicită, asupra căreia pot avea un impact mai mulți factori.
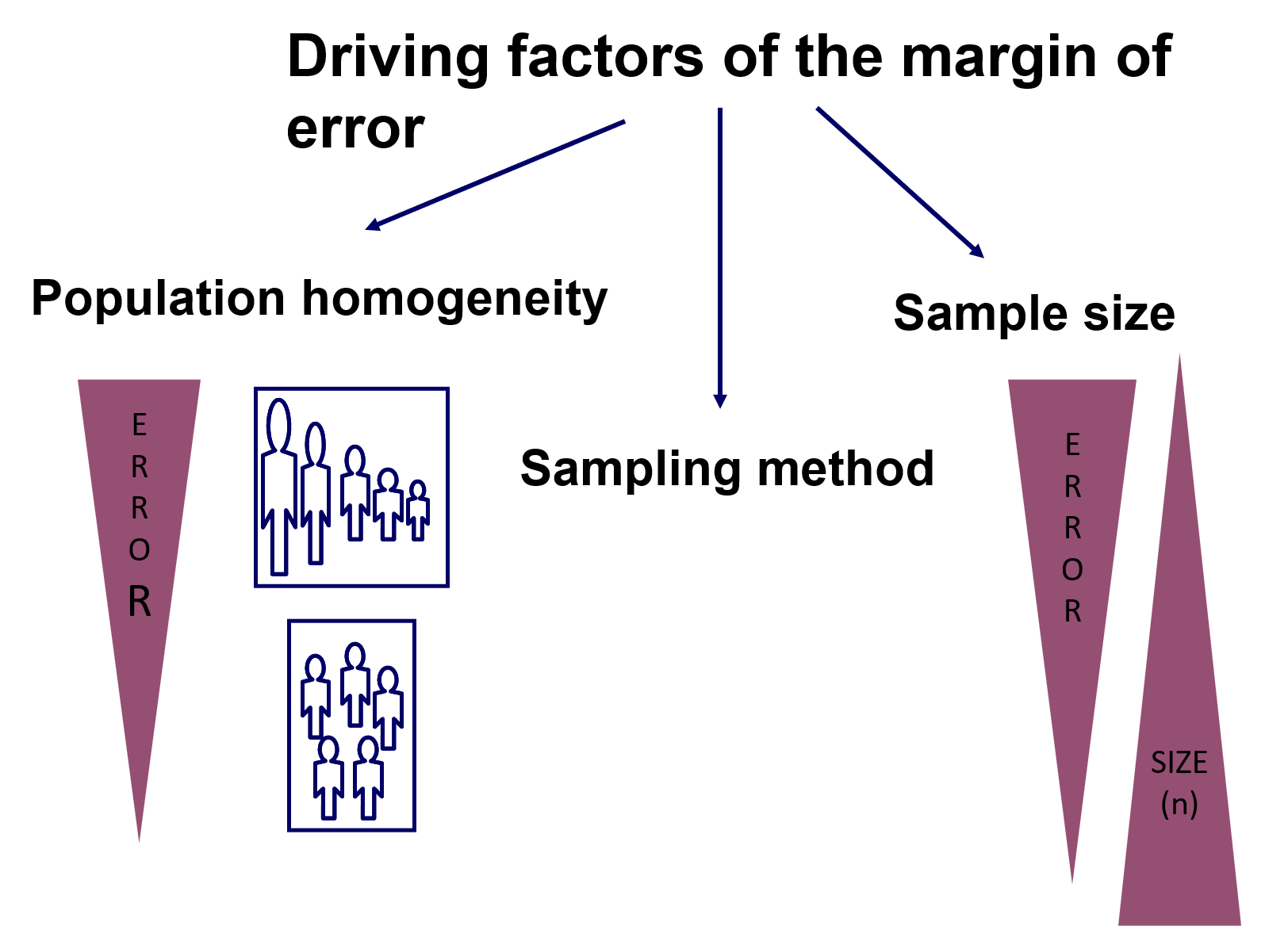
Marja de eroare va depinde, în principiu, de trei factori determinanți:
a. Cât de omogene sunt datele în cadrul populației: cu cât sunt mai eterogene, toate celelalte lucruri fiind egale, cu atât marja de eroare este mai mare.
b. Marimea eșantionului: cu cât dimensiunea este mai mică, toate celelalte lucruri fiind egale, cu atât marja de eroare este mai mare.
c. Tehnica de eșantionare: se alege în funcție de caracteristicile datelor dumneavoastră.
Nu putem face prea multe în ceea ce privește punctul (a), dar există o anumită posibilitate de a interveni la punctele (b) și (c). În ceea ce privește punctul (c), este important de menționat că există o mare varietate de tehnici de eșantionare disponibile pe care le putem aplica. Diagrama de mai jos prezinta aceasta varietate in termini vizuali:
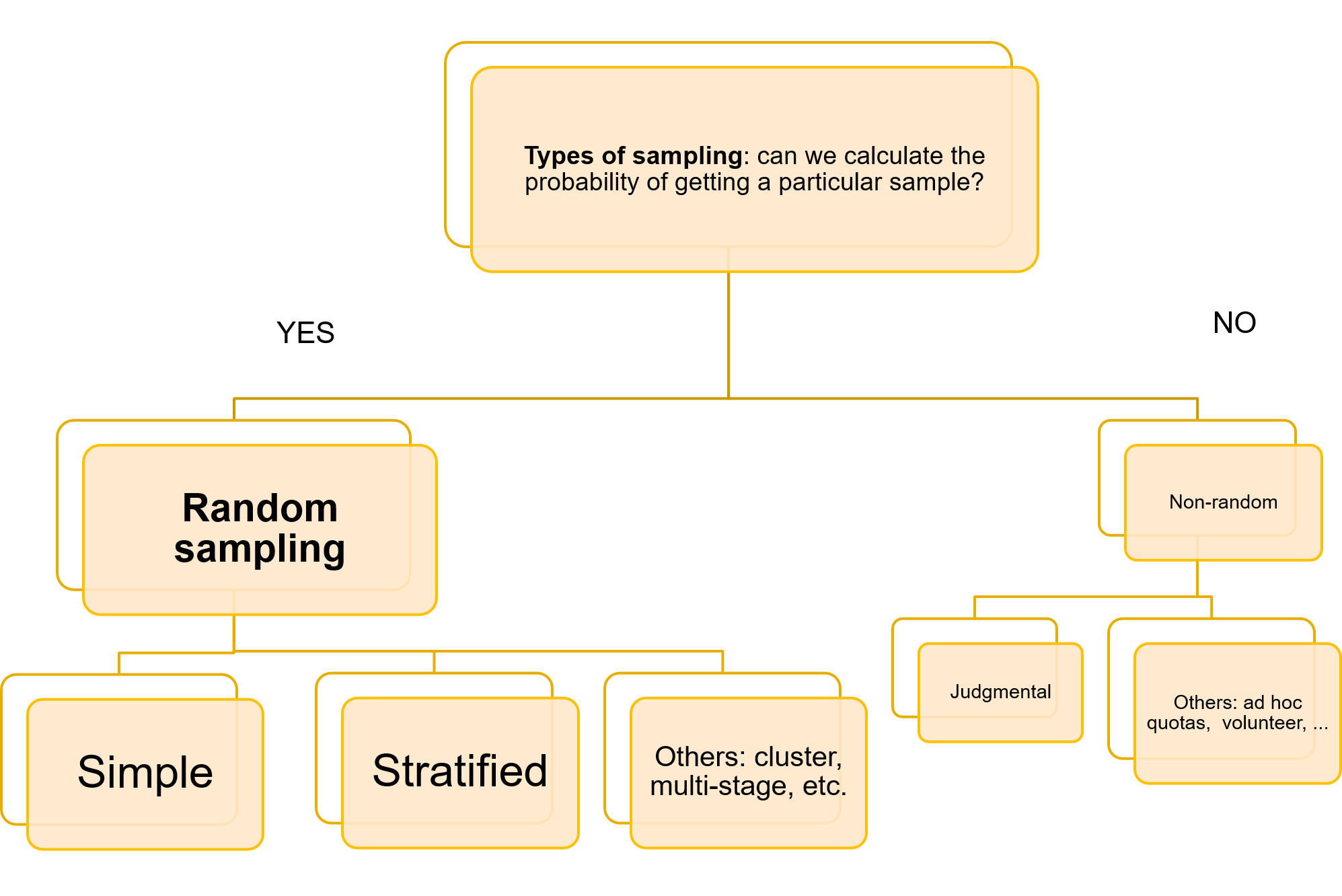
Putem controla marja de eroare a concluziilor noastre doar dacă lucrăm cu eșantioane aleatorii, iar cele mai frecvente tehnici de eșantionare aleatorie sunt eșantionul aleatoriu simplu și eșantionul aleatoriu stratificat.
Tehnici de eșantionare
Eșantionare aleatorie simplă Click to read 
Eșantionarea aleatorie simplă este cea mai elementară tehnică de eșantionare care se bazează pe selectarea aleatorie a observațiilor studiate. Ea constă în selectarea aleatorie a n unități din populație, pornind de la o listă de unități ale populației. Dar chiar și în cadrul acestei tehnici simple, se pot decide unele particularități ale procesului de selecție aleatorie. De exemplu, putem decide dacă eșantionarea va avea loc cu sau fără înlocuire. În cazul în care eșantionarea se realizează cu înlocuire, aceasta înseamnă că fiecare unitate selectată aleatoriu pentru a face parte din eșantion este repusă în populație după fiecare tragere la sorți a selecției aleatorii. Acest lucru implică, în mod evident, că o unitate poate fi selectată de mai multe ori, dar garantează că condițiile în care are loc fiecare extragere de selecție sunt egale și constante, iar rezultatele fiecăreia dintre ele sunt independente una de cealaltă.
Dimpotrivă, în cazul în care se efectuează o eșantionare aleatorie simplă fără înlocuire, fiecare unitate este eșantionată o singură dată, dar nu putem garanta că condițiile sunt constante de-a lungul selecției. Eșantionarea cu și fără înlocuire poate produce rezultate semnificativ diferite pentru populațiile mici. Ele sunt echivalente numai dacă dimensiunea populațiilor (N) este foarte mare.
Eșantionare stratificată Click to read 
În multe ocazii, observațiile sunt grupate în mod natural pe baza caracteristicilor pe care le au în comun. De exemplu, datele privind distribuția salariilor sunt grupate în funcție de sectorul economic al lucrătorilor, de sexul acestora sau de regiunea de reședință. Straturile sunt definite ca părți ale populației de interes care prezintă o mare omogenitate internă, chiar dacă există o mare variabilitate între straturi. Eșantionarea stratificată profită de aceste grupări ale observațiilor și selectează aleatoriu un număr de unități pe fiecare strat L (nL), astfel încât dimensiunea totală a eșantionului să fie obținută prin însumarea elementelor eșantionate pe fiecare strat. Există mai multe criterii de repartizare a mărimii totale a eșantionului pe straturi, cele mai frecvente fiind următoarele:
- Uniform: aceeași dimensiune a eșantionului pe orice strat
- Proporțional: proporția membrilor eșantionului este aceeași cu proporția membrilor populației din fiecare strat.
- Optim: proporțional cu mărimea și eterogenitatea (varianța) pe fiecare strat.
În aceleași condiții și cu aceleași cerințe de precizie și încredere, putem afirma că, în general, eșantionarea stratificată necesită o dimensiune mai mică a eșantionului decât eșantionarea simplă, dar aspectele legate de calcularea dimensiunilor eșantionului vor fi detaliate la punctul următor.
Calcularea mărimii optime a eșantioanelor
Calculating Optimal Sample Sizes Click to read 
The golden rule in terms of relating the sample size with the precision of our estimates is that the larger the same size, all other things being equal, the smaller the margin of error. However, getting statistical data, even if it is in the form of a sample, can be costly and sometimes we do not have resources to have large samples. As a consequence, there is a compromise solution that sets the optimal (minimum) sample size that we need, given our requirements in terms of precision (margin of error) and confidence of our estimates, and the heterogeneity (variance) of the variable of interest in the population.
|
Regula: cu cât dimensiunea eșantionului este mai mare, cu atât marja de eroare este mai mică
|
|
 |
|
Soluție pentru eșantionare simplă Click to read 
Să presupunem mai întâi că dorim ca eșantionul nostru să estimeze o medie a populației pentru o variabilă continuă, iar eșantionul nostru va fi selectat prin eșantionare aleatorie simplă. Formulele pe care trebuie să le aplicăm sunt următoarele:
Constanta 𝑘 provine dintr-o distribuție normală și devine mai mare dacă creștem nivelul de încredere dorit, iar simbolul 𝑒 reprezintă marja de eroare pe care suntem dispuși să ne-o asumăm. În plus, trebuie să facem și o presupunere privind omogenitatea variabilei în populație. Acest lucru implică faptul că trebuie să impunem o valoare realistă (de obicei provenind dintr-un studiu anterior) pentru varianța 𝜎2 a populației.
În aceste ecuații, 𝑛* este soluția pentru o eșantionare aleatorie simplă cu înlocuire, 𝑛 este soluția pentru o eșantionare aleatorie simplă fără înlocuire, iar N este dimensiunea populației. În general, n*≥n, iar ambele soluții converg atunci când N este foarte mare.
În mod similar, dacă ne interesează să estimăm proporția (P) de unități dintr-o populație care dețin o anumită caracteristică, formulele necesare pentru a găsi dimensiunile optime ale eșantionului în această tehnică de eșantionare sunt:
Din nou, constanta 𝑘 provine dintr-o distribuție normală și devine mai mare dacă creștem nivelul de încredere dorit, iar termenul 𝑒 reprezintă marja de eroare pe care suntem dispuși să ne-o asumăm. În acest caz, Trebuie să facem și o presupunere privind valoarea lui P*(1-P), care reprezintă varianța unei variabile binare (da/nu). Soluția obișnuită este să presupunem că P=1-P=0,5, astfel încât P*(1-P)=0,25 ia valoarea maximă.
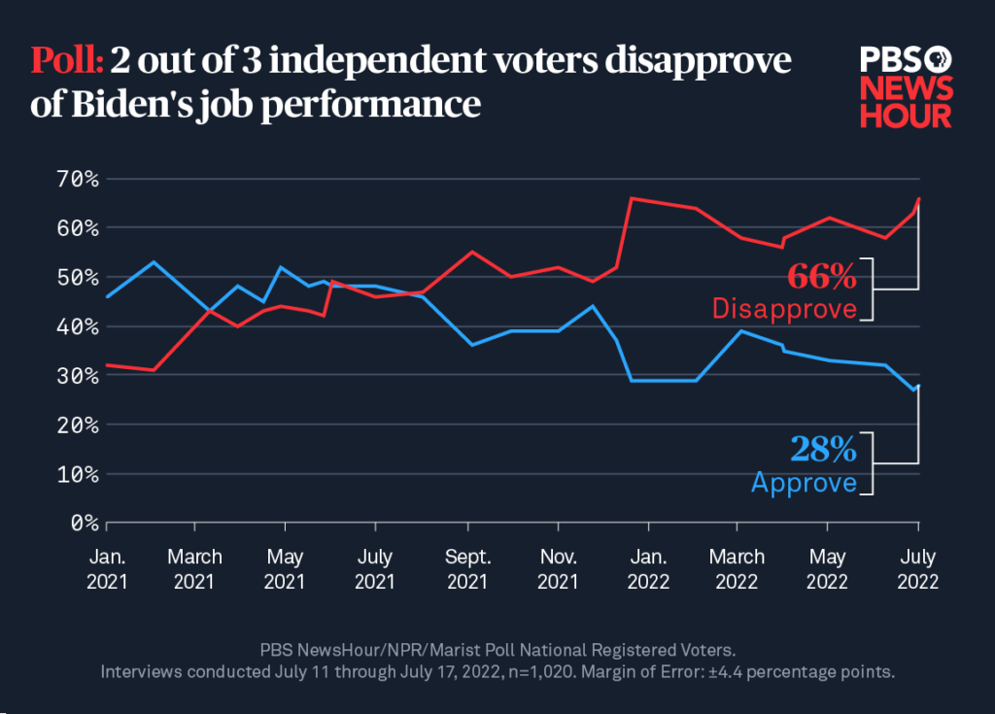
Putem ilustra această tehnică prin prezentarea unui exemplu practic privind modul în care se determină dimensiunile eșantioanelor și cum ne poate ajuta aplicarea R în această privință: Serviciul public de radiodifuziune (PBS) din SUA estimează în mod regulat procentul de cetățeni care aprobă sau dezaprobă activitatea președintelui. În cazul președintelui Joe Biden, aceștia efectuează aceste sondaje din luna ianuarie 2021. Următorul grafic arată evoluția estimărilor lor:
Într-un sondaj recent din această serie, PBS a dorit să aibă estimări cu un nivel de încredere de 99%, a fost dispus să aibă o marjă de eroare de ±4,4% și a presupus cel mai rău scenariu (soluția obișnuită) și a presupus că procentul de oameni care aprobă (P) este același cu procentul de oameni care nu aprobă (1-P). Care ar fi numărul de cetățeni care ar trebui să fie eșantionați în aceste condiții? Ecuațiile afișate mai sus pot fi implementate în limbajul R pentru a găsi o soluție.
Mai întâi trebuie să instalăm și să încărcăm pachetele necesare:
Mai departe, putem găsi această dimensiune optimă a eșantionului prin apelarea funcției "sample.size.prop" din pachet. Această funcție permite o eșantionare cu sau fără înlocuire, deși nu se vor găsi diferențe practice între soluția acestor două alternative, având în vedere dimensiunea mare a populației (N) din care sunt extrase eșantioanele (putem presupune în mod arbitrar că N=200.000.000). Următoarele părți de cod calculează soluțiile respective pentru o eșantionare fără și cu înlocuire:
În ambele cazuri, se găsește ca soluție o dimensiune a eșantionului de aproximativ 1.000 de unități.
Soluție pentru eșantionarea stratificată Click to read 
În acest capitol se detaliază formulele de calcul al mărimilor eșantioanelor în cazul eșantionării stratificate. Din rațiuni de simplitate și claritate, ne vom axa doar pe cazul estimării mediei unei populații și vom oferi cele mai frecvente două soluții, care corespund cazurilor de repartiție proporțională (1) și repartiție optimă (2):
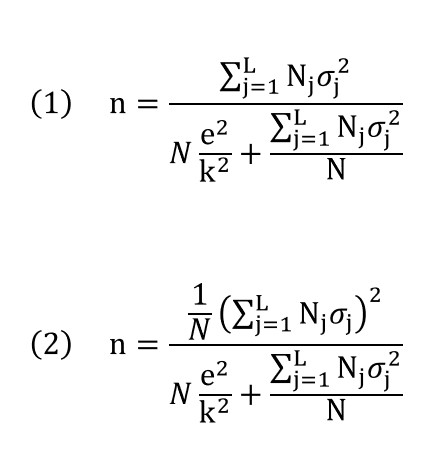 |
După cum s-a comentat mai sus, în ambele cazuri, formula corespunde estimării mediei populației pentru o variabilă continuă cu o eșantionare stratificată fără înlocuire. În aceste expresii, Nj reprezintă dimensiunea stratului j și 𝜎2j reprezintă varianța variabilei pe același strat.
În mod similar cu soluțiile detaliate pentru eșantionarea aleatorie simplă, putem ilustra modul în care se calculează dimensiunile optime ale eșantioanelor în cazul eșantionării stratificate prin prezentarea unui exemplu practic cu ajutorul limbajului R.
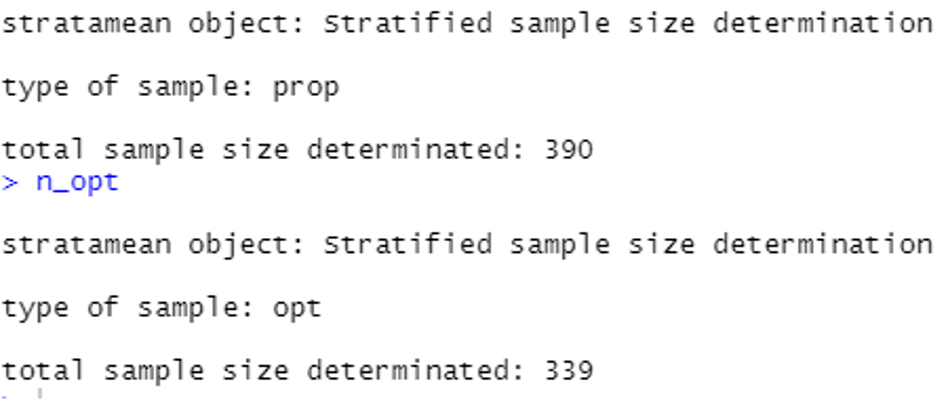
Să presupunem că o organizație de caritate efectuează un sondaj prin sondaj pentru a studia donațiile anuale făcute de membrii săi, care sunt clasificați în trei grupe diferite în funcție de vârsta lor, cu 100, 700 și 200 de membri fiecare. În urma unui studiu pilot, această organizație caritabilă știe că abaterile standard respective (𝜎j) ale donațiilor anuale din fiecare grup sunt de 6, 30 și 12 EUR. Dorim să aflăm dimensiunea minimă a eșantionului necesar pentru a estima donația anuală medie, stabilind o marjă de eroare de 2 EUR și un nivel de încredere de 95%.
Următoarele linii de cod vor calcula dimensiunea optimă a eșantionului, oferind soluțiile pentru cazul unei alocări proporționale și optime, prin apelarea funcției "stratasize" inclusă în pachetul "samplingbook" din R:
 |
Soluțiile respective sunt de 390 și 339 de unități, după cum se detaliază mai jos:
În cele din urmă, putem să ne întrebăm care dintre aceste două mărimi de eșantion vor fi alocate între straturi, Acest lucru poate fi făcut prin apelarea funcției "stratasamp" din același pachet:
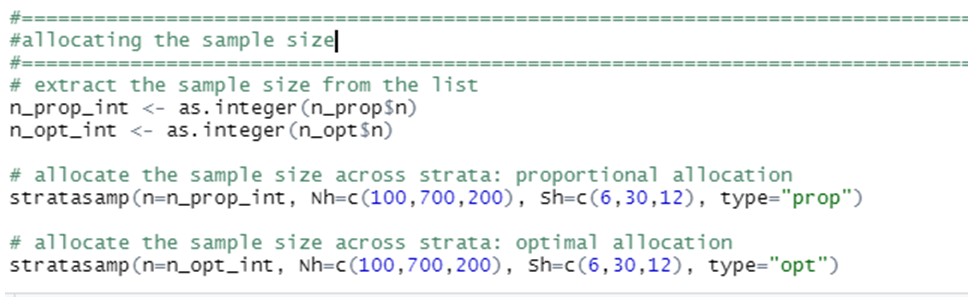
Rezultă soluțiile:

|
 Redare audio
Redare audio